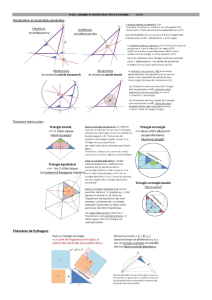
Trigonométrie 1º) Sinus, cosinus et tangente Définition : Dans un

Trigonométrie Dans un triangle rectangle, si on fait un
1º) Sinus, cosinus et tangente agrandissement ou une réduction,
d'après le théorème de Thalès,
les rapports des longueurs des côtés ne changent pas,
ils ne dépendent que des angles aigus du triangle.
Définition : Dans un triangle ABC rectangle en A,
cos
̂
C=côté adjacent à
̂
C
hypoténuse =AC BC
sin
̂
C=côté opposé de
̂
C
hypoténuse =AC BC
tan
̂
C=côté opposé de
̂
C
côté adjacent à
̂
C
=AC
BC
On met la calculatrice en mode degré. On tape : cos 30 = et il s'affiche :
0.866025403 et on écrit sur sa copie : cos 30º ≈ 0,87 (arrondi au centième).
Calcul de l'angle A tel que sin A = 0,7 : on tape à la calculatrice :
2nd sin-1 0.7 = et il s'affiche : 44.427004 et on écrit sur sa copie : A ≈ 44,43.
2º) Propriétés
Prop. : quel que soit l'angle aigu x, cos x et sin x sont des nombres entre 0 et 1.
Démonstration : d'après Pythagore, l'hypoténuse (le côté opposé de l'angle droit) est
toujours le plus grand côté d'un triangle rectangle, donc les rapports de longueur de
dénominateur l'hypoténuse sont inférieurs à 1.
Propriété : Lorsque deux angles sont complémentaires,
le sinus de l'un est égal au cosinus de son complémentaire.
Démonstration : la somme des 3 angles d'un triangle vaut 180º donc les deux angles
aigus d'un triangle rectangle sont complémentaires (car leur somme vaut 90º). Soit ABC
un triangle rectangle en A (voir ci-dessus) :
cos
̂
C=côté adjacent à
̂
C
hypoténuse =AC BC =côté opposé de
̂
B
hypoténuse =sin
̂
B
cos
̂
B=côté adjacent à
̂
B
hypoténuse =AB BC =côté opposé de
̂
C
hypoténuse =sin
̂
C
.
Propriété : quel que soit l'angle aigu x,cos2 x + sin2x = 1
Note : cos2 x désigne (cos x)2 (le carré du cosinus de l'angle x).
(La démonstration de la propriété précédente utilise le théorème de Pythagore).
Propriété : quel que soit l'angle aigu x,
tan x=sin x
cos x
.
AC
Bhypoténuse
Côté opposé
de l'angle C
Côté adjacent
de l'angle C