Exercice n°4 (1,5 points )

Groupement académique du Grand Est
MATHEMATIQUES
Exercice n°1 ( 1,5 points )
1) Calculer la valeur exacte et donner un encadrement à 10-3 du nombre x :
x =
3
32
106
10102
2) On donne A ( x ) = 5( 1 – x ) – ( 1 – x )( x + 3 )
a) Factoriser A ( x )
b) Résoudre l’équation ( 1 – x )( 2 – x )
Exercice n°2 ( 5 points )
Un avion, en vol, est soumis à une force appelée traînée de valeur R
R =
2
1
v² S Cx
R : traînée en N
: masse volumique de l’air en kg / m3 : = 1,225 kg / m3
S : surface des ailes en m² : S = 16 m²
v : vitesse en m /s
Cx : Coefficients de traînée : Cx = 0,08
1) Calculer R pour une vitesse de 72 m /s. Donner le résultat arrondi à l’unité.
2) Exprimer R en fonction de v
3) En prenant R = 0,78 v²
a) Compléter le tableau de valeurs :
v
0
20
30
40
50
80
R
b) Représenter graphiquement R en fonction de la vitesse v pour v compris entre 0 et 80
Echelle ; en abscisse 1cm pour 10 m /s et en ordonnée 1 cm pour 500 N
c) Quel est le nom de la courbe obtenue ?
d) Déduire du graphique en faisant apparaître les constructions utilisées pour la lecture
- La traînée R correspondant à une vitesse de 55 m /s
- La vitesse associée à une traînée de 3500 N.
Exercice n°3 (2 points )
On relève la taille de 250 élèves d’un lycée
1) Compléter le tableau statistique suivant :
Taille
( en cm )
Effectif
ni
Fréquence
fi ( en % )
Effectif cumulé
croissant
Centre
xi
Produit
xi ni
[ 145 ; 155 [
10
[ 155 ; 165 [
73
29,2
98
160
11680
[ 165 ; 175 [
33,6
[ 175 ; 185 [
64
[ 185 ; 195 [
TOTAUX
2) Calculer la taille moyenne d’un élève par la méthode de votre choix.
3) Donner le nombre d’élèves dont la taille est inférieure à 175 cm.
Exercice n°4 (1,5 points )
Sur une carte à l’échelle 1/200 000, trois villes A, B et C forment un triangle tel que :
AB = 80 mm ; AC = 50mm ; BAC = 113°
1) Construire le triangle ABC
2) Calculer en mm, le mesure de BC. Donner le résultat à l’unité
3) Calculer, en km, la distance réelle entre A et B.
BEP 1999
Secteur 3

SCIENCES PHYSIQUES
Exercice n°5 (3,5 points )
Le butane C4H10 brûle dans le dioxygène O2 selon l’équation suivante :
2 C4H10 + 13 O2  _ _ _ CO2 + 10 H2 O
1) Nommer les produits de la réaction.
2) Equilibrer la réaction ci-dessus en complétant le nombre de moles de CO2.
3) Calculer la masse d »une mole d’eau
4) On brûle 10 L de gaz butane.
Calculer le volume de dioxygène nécessaire et la masse d’eau obtenue.
On donne : M (H) =1 g / mol ; M (O) =16 g / mol
Volume molaire dans les conditions de l’expérience : 24 L / mol
Exercice n°6 (3,5 points )
En fonctionnement , une lampe de poche est assimilable à un circuit constitué :
- D’un dipôle résistif de résistance R = 4,7  ;
- D’une pile alcaline LR03 qui fournit une tension U = 1,34V
- D’un interrupteur
1) Schématiser ce circuit
2) Calculer l’intensité du courant dans le circuit
3) Calculer la puissance dissipée dans le dipôle résistif .
4) Calculer ( en J et en Wh ) , l’énergie dissipée dans le dipôle résistible au bout de 2h15min .
Exercice n°7 (3 points )
Une grue possède un contre poids  , de centre de gravité A .
La masse de  est de 1000 kg .
Une charge est suspendue en B . Son poids est de 2000 N .
On négligera la masse de la barre AB 
A O  B
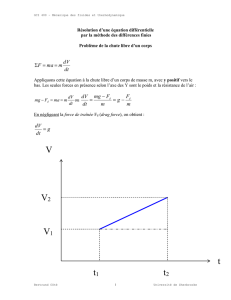
1) Calculer la valeur du poids de  ( on donne g = 10 N / kg )
2) Compléter le tableau des caractéristiques des trois forces exercées sur la barre AB
Point
d’application
Droite
d’action
Sens
Valeur
(En N)
F
1/4
F
2/4
F
3/4
.
3) La charge  , de poids 2000 N , s’élève de 20 mètres en 12 secondes .
a) Calculer le travail mécanique nécessaire .
b) Calculer la puissance fournie par le moteur de la grue .