Applications

Chapitre 2 : Dérivation TES
I. Tangente et nombre dérivé
Aux origines la dérivation, était un problème purement géométrique : il s'agissait de connaître le coefficient directeur
ou pente d'une droite particulière à une courbe qu'on appelle la tangente .
Cette pente est aussi appelée nombre dérivé de la fonction f en a . Il est noté f ’(a) .
Quand il existe, on dit que la fonction f est dérivable en a .
 f est une fonction définie sur un intervalle I . a et x = a + h sont deux valeurs distinctes de I .
A ( a, f (a)) et M ( x, f (x)) sont deux points de la courbe représentative de la fonction. Le coefficient directeur de la sécante (AM)
à la courbe est
(x) ( )
x
f f a
ma
, c’est le taux de variation de la fonction entre a et x .
Lorsque M devient de plus en plus proche de A , mais M  A et si m a une limite quand x tend vers a alors :
cette limite est le coefficient directeur de la tangente en A à la courbe.
Le coefficient directeur de la tangente en A à la courbe est
x
(x) ( )
' lim x
a
f f a
fa a
pourvu que cette limite existe.
En posant x = a + h on obtient :
0
( ) ( )
'( ) lim
h
f a h f a
fa h
.
La limite finie de l’accroissement moyen de la fonction f entre a et x = a + h , quand h tend vers 0,
est le nombre dérivé de f en a, noté
x
(x) ( )
' lim x
a
f f a
fa a
ou
0
( ) ( )
'( ) lim
h
f a h f a
fa h
Ex : Déterminer le nombre dérivé en a = 1 de la fonction f définie par : f (x) =2x2 + 1
Pour trouver ce nombre, à l’aide de la définition d'un nombre dérivé : j’étudie la limite lorsque x tend vers 1 du quotient
2 2 2
x 1 x 1 x 1
2x 1 3 2x 2 x 1
2. 2. 2. x 1
x 1 x 1 x 1 x 1 x 1
ff  
donc lorsque x tend vers 1 ,
le quotient
x1
x1
ff
tend vers 2 × (1 + 1) = 4 , f (x) = 2x2 +1 est dérivable en a = 1 et f ’(1) = 4 .
 Le nombre dérivé de f en a étant le coefficient directeur de la tangente à la courbe de f au point A d’abscisse a
nous pouvons en déduire l’équation de la tangente à la courbe au point A
Soit A ( a, f (a)) un point de la courbe représentative de la fonction f ,
l’équation de la tangente en A à la courbe est : y = f ’(a) .( x  a ) + f (a)
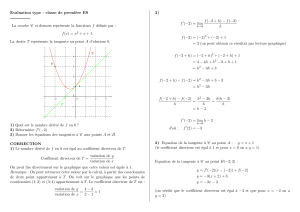
Ex : Soit f la fonction définie sur  par f (x) = x 2 . Quelle est l’équation de la tangente au point M d’abscisse  2 ?
le coefficient directeur de la tangente en M est :
22
00
22
0 0 0
( 2 ) ( 2) ( 2 ) ( 2)
'( 2) lim lim
4 4 4 4
lim lim lim 4 4
hh
h h h
f h f h
fhh
h h h h h
hh
l’équation de la tangente en M est : y = f ’( 2)  ( x + 2 ) + f (2)
soit y =  4  ( x + 2 ) + 4 et y = – 4 x – 4
___________
A
M
A
M
A
O
O
O
a
a
x
x = a + h
h
h
h
O
M

Remarque : la courbe représentative d’une fonction f peut avoir une tangente en un point a sans que la fonction soit dérivable en a
la courbe représentative de la fonction racine carrée est tangente à la droite d’équation x = 0 en 0
or la fonction racine carrée n’est pas dérivable en 0 :
en effet
00
00
lim lim
hh
hh
hh
ce n’est pas une limite finie donc la fonction n’est pas dérivable en 0.
II. Fonction dérivée
imaginons qu’une fonction f soit dérivable sur tout un ensemble I
cela signifie que tout réel x de cet ensemble I, il existe un nombre dérivé f ’(x)
f est une fonction dérivable sur un ensemble I , la fonction dérivée de la fonction f est la fonction notée f ’
et définie pour tout réel x de I par : f ’ : x nombre dérivé de f en x = f ’(x)
Théorème : si une fonction est dérivable en a , alors elle est continue en a ( admis en TES )
Attention la réciproque du théorème est fausse :
soit
(x) xf
f est continue en 0. Montrons que f n’est pas dérivable en 0 .
0 0 0 0
00
(0 ) (0)
lim (x) lim lim lim 1
h h h h
hh
f h f
fh h h
0 0 0 0
00
(0 ) (0)
lim(x) lim lim lim 1
h h h h
hh
f h f
h h h
.
les limites à droite et à gauche sont différentes, donc f ’(0) n’existe pas .
dériver f (x) ou calculer la dérivée de f (x) signifie trouver l’expression de f ’(x) .
dans certains cas nous avons des formules qui permettent le calcul de la dérivée sans utiliser la définition.
III. Dérivées des fonctions usuelles
Fonction
Dérivée
Ensemble de dérivation
k
0
;    
x
1
;    
x2
2.x
;    
x3
3.x2
;    
xn
n . xn-1
;    
1
x
2
1
x
; 0 0 ;    
x
1
2x
0 ; 
O
O

IV. Opérations sur les dérivées
u et v sont des fonctions dérivables sur l’intervalle I ,
λ
est une constante réelle , u’ et v’ sont les fonctions dérivées respectives de u et v.
Fonction
Dérivée
.u
.u’
u + v
u’ + v’
uv
u’v + uv’
Error!
Error!
Error!
Error!
Ex : soit
32
(x) x 1 2x 8x 5f   
calculer f ’(x) : On pose : u(x) = x 3 + 1 et v(x) = 2x 2  8x + 5 d’où f = uv et f’ = u’ v + v’ u
avec u’(x) = 3x 2 et v’(x) = 4x  8 .
2 2 3
'(x) 3x 2x 8x 5 4x 8 x 1f     
f ’(x) =10x 4  32x 3 + 15x 2 + 4x  8
Ex : soit
2
2
x 2x 1
(x) x1 f
calculer f ’(x),
puis déterminer les abscisses des points de la courbe de f pour lesquels la tangente est parallèle à l’axe des abscisses.
a) je pose : u(x) = x 2  2x 1 et v(x) = x 2 + 1 d’où f =
u
v
et f’ =
2
''u v uv
v
avec u’(x) = 2x  2 et v’(x) = 2x.
22 3 2 3 2
22
22
2x 2 x 1 2x x 2x 1 2x 2x 2x 2 2x 4x 2x
'(x) x 1 x 1 f          
soit
2
2
2
2 x 2x 1
'(x) x1 f
b) une tangente à la courbe parallèle à l’axe des abscisses a un coefficient directeur nul.
je dois donc résoudre f ’(x) = 0.
or les racines du polynôme du second degré x 2 + 2x  1 sont : x 1 =  1 
2
et x 2 =  1 +
2
la courbe de f admet deux tangentes « horizontales » aux points d’abscisses :
x 1 =  1 
2
et x 2 =  1 +
2
V. Dérivée et variations
dans ce paragraphe nous allons utiliser le signe de la dérivée pour étudier les variations de la fonction f .
sens de variation et signe de la dérivée : f est une fonction définie et dérivable sur un intervalle I
en x = 1,
la fonction sinus est croissante.
la pente de la tangente est positive.
en x =
2
,
f n'est ni croissante, ni décroissante
la pente de la tangente est nulle.
en x = 3, la fonction sinus est décroissante.
la pente de la tangente est négative.
 si en tout point de I , f’ = 0 alors f est constante sur I.
 si en tout point de I , f’  0 alors f est décroissante sur I.
 si en tout point de I , f’  0 alors f est croissante sur I.
Remarque : si f ’ > 0 sur un intervalle ] a ; b[, sauf en un nombre fini de points où f ’ s’annule, alors f est strictement croissante
Ex : f est définie sur  par :
3
(x) 2x 1f
, la dérivée de la fonction g est : g ’(x) = 6x 2 d’où g ’  0 or g ’ ne s’annule qu’en 0 :
la fonction g est strictement croissante sur  .
extremum :
soit c un point du domaine de définition d’une fonction f .

 f (c) est un maximum relatif de f s’il existe un ouvert ] a ; b [ contenant c tel que f (x)  f (c) pour x ] a ; b [.
 f (c) est un minimum relatif de f s’il existe un ouvert ] a ; b [ contenant c tel que f (x)  f (c) pour x ] a ; b [.
Remarque : le terme local est justifié par le fait que la fonction n’est considérée que sur un intervalle ouvert
suffisamment petit autour de c pour que , f (c) soit la plus grande (ou la plus petite) valeur cet intervalle.
il est possible qu’en dehors de cet intervalle f atteigne des valeurs plus grandes (ou plus petites).
un maximum ou un minimum relatif de f est un extremum relatif .
Théorème : soit f une fonction dérivable sur] a ; b [ ,
si la dérivée de f s’annule en une valeur c de l’intervalle ] a ; b [, en changeant de signe,
alors la fonction f admet f (c) pour extremum local atteint en c
Ex : f est la fonction définie sur  par :
32
(x) x 1,5x 6x 3f   
.
22
'(x) 3x 3x 6 3(x x 2)f     
, or f ’ est une fonction polynôme du second degré qui s’annule pour
1
x2
ou
2
x1
.
x
+
f ’(x)
+
–
+
f (x)
Sur l’intervalle ]   ; 1 [, la dérivée s’annule pour
1
x2
en outre f ’(x) > 0 pour x <  2 et f ’(x) < 0 pour 2 < x < 1. f admet un
maximum f (2) = 7 sur l’intervalle ]   ; 1 [.
VI. Dérivée d’une fonction composée
Théorème ( admis ) : g est une fonction dérivable sur un intervalle J.
u est une fonction dérivable sur un intervalle I tel que pour tout x  I, u(x) J.
alors la fonction
f g u
est dérivable sur I et pour tout x de I :
'(x) ' [ (x)] '(x)f g u u
Ex : f est la fonction définie sur  par
2
2
(x) 3x 2x 1f  
.
f g u
avec
(x) 3x² 2x 1u  
, et g la fonction
2
uu
d’où
'(x) ' (x) '(x)f g u u
d’autre part
'(x) 6x 2u
et
'( ) 2g u u
ainsi
' (x) 2 3x² 2x 1 6x 2f    
Applications
Fonction
Dérivée
un
n.un-1×u’
u
u'
2u
Ex :
 f est la fonction définie sur  par
3
(x) 2x 3f
.
3
fu
avec
(x) 2x 3u
, d’où
2
' 3 'f u u
comme
'(x) 2u
nous obtenons
2
'(x) 6(2x 3)f
 f est la fonction définie sur  par
21
(x) x1 f
.
1
fu
avec
2
(x) x 1u
, d’où
2
'
'u fu
comme
'(x) 2xu
nous obtenons
2
2
2x
'(x) x1 f
 f est la fonction définie sur  par
2
(x) x x 1f  
.
fu
avec
2
(x) x x 1u  
, d’où
'
'2
u
fu
comme
'(x) 2x 1u
nous obtenons
2
2x 1
'(x) 2 x x 1 f
0
–2
0
1
0