Les triangles : propriétés

Les triangles : propriétés
Sommaire :
1. Sommes des angles
2. médiatrices et cercle circonscrit
3. droites particulières
1. Somme des angles d’un triangle
Somme des angles : Faire varier les points et additionner les mesures des angles pour deux ou trois triangles.
Que constate-on ?
Propriété : Dans tous les triangles, la somme des mesures des trois angles est égale à 180°.
Remarque : On démontrera cette propriété dans le chapitre sur les angles.
Application aux triangles particuliers :
- Dans un triangle équilatéral, les angles valent 60°.
- Dans un triangle rectangle, la somme des deux angles non droits, valent 90°
- Dans un triangle isocèle, si on connaît un angle, on connaît les trois.
- Dans un triangle rectangle isocèle, les angles valent 45° et 90°.
Exemple : Calculer les angles à la base d’un triangle isocèle dont l’angle au sommet vaut 135°.
Exercices 27 à 36 p 200 65,66 p 204
2. Médiatrice et cercle circonscrit
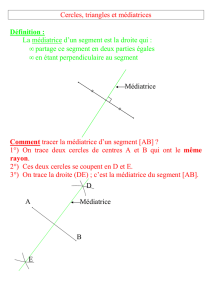
a) Médiatrice d’un segment
Définition : La médiatrice d’un segment est une droite qui passe par le milieu d’un segment et qui lui est
perpendiculaire.
Tracer un segment [AB] et sa médiatrice.
Remarque : Il existe deux façons de tracer une médiatrice
1. A la règle et au compas 2. A la règle graduée et à l’équerre
Propriétés : La médiatrice d’un segment est l’ensemble des points équidistants aux extrémités du segment.
Si une droite passe par deux points situés à égale distance des extrémités d’un segment, alors cette
droite est la médiatrice de ce segment.
b) Médiatrice d’un triangle
Définition : Une médiatrice d’un triangle est une droite qui est médiatrice d’un de ses côtés. Il y a donc trois
médiatrices dans un triangle.
Figure :

AB
C
OO
A
19, 20 p 139
Démonstration concourante et équidistance par apport aux sommets.
Propriété : Les médiatrices d’un triangle sont concourantes Le point de concours des médiatrices est centre du
cercle circonscrit au triangle.
22, 23, 24 p 139
3. Droites particulières d’un triangle
Remarque : Les hauteurs (vu dans le chapitre précédent) et les médiatrices sont aussi des droites particulières
du triangle.
a) Médiane
Définition : La médiane est une droite passant par le sommet d’un triangle et par le milieu du côté opposé
Comme pour les hauteurs, on dit médianes issue … de ou issue du sommet …
Figure :
AB
C
I
JK
G
36 p 140
b) Bissectrice
Définition : On appelle bissectrice d’un angle, la demi-droite qui partage cet angle n deux angles de même
mesure.
Figure :
A
B
C
I
27, 28, 29 p 140
Exercices complémentaires (DM ?) 45, 46, 48.