STATISTIQUES SERIES STATISTIQUE A UNE VARIABLE Les

1
STATISTIQUES
SERIES STATISTIQUE A UNE VARIABLE
Les premières études statistiques étaient d’ordre démographique, on en a conservé le vocabulaire.
1. Vocabulaire
Réaliser une étude statistique consiste à classer les individus d’une population en fonction d’un caractère.
Exemples :
Classer les élèves d’une classe en fonction de leur âge.
Classer les voitures garées sur un parking en fonction de leur couleur.
Classer les joueurs d’une équipe de foot en fonction de leur poste.
Classer des forfaits d’un opérateur téléphonique en fonction de leur prix.
On dit que le caractère étudié est quantitatif quand les valeurs du caractère sont des tailles, des durées, des prix…,
c'est-à-dire des quantités mesurables. (Un caractère quantitatif est discret si les valeurs sont ponctuelles. Un
caractère quantitatif est continu si les valeurs sont regroupées en intervalles, en classes.)
On dit que le caractère étudié est qualitatif quand les valeurs sont des opinions, des comportements, des couleurs,
des lieux…c'est-à-dire des« qualités » d’un individu.
Une fois que le caractère de la série statistique est posé, on peut définir :
 L’effectif d’une valeur d’un caractère est le nombre d’individus de la population qui ont cette
valeur.
 L’effectif total est le nombre d’individus de la population ; il est égal à la somme des et sera noté N
dans la suite du cours.
Exemple : « élèves d’une classe en fonction de leur âge »
Âge (caractère)
14
15
16
17
TOTAL
Effectif
1
27
5
2
35

2
 La fréquence d’une valeur est le quotient de l’effectif de cette valeur par l’effectif total, c'est-à-dire :
.
Remarque : La fréquence est toujours comprise entre 0 et 1. On peut l’exprimer en pourcentage en la multipliant
par 100.
 L’effectif cumulé croissant (resp décroissant) de est la somme des effectifs des valeurs inférieures
(resp supérieures) ou égales à .
 La fréquence cumulée croissante (resp décroissante) de est la somme des fréquences des valeurs
inférieures (resp supérieures) ou égales à .
Exemple : « élèves d’une classe en fonction de leur âge »
EXERCICE 1 :
Une étude statistique a été effectuée sur un échantillon de population. Le caractère étudié est la Taille des individus.
Pour chaque taille, on a indiqué le nombre de personnes correspondant.
Taille
1,65
1,66
1,67
1,68
1,69
1,70
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,90
1,91
1,92
1,93
1,94
Total
Effectif
2
1
4
3
6
10
6
2
7
13
17
12
10
9
11
8
5
3
6
3
4
1
1
0
2
3
1
0
1
0
151
a. Effectuer le regroupement en classes de ces résultats :
Taille
1,65 à 1,69
1,70 à 1,74
1,75 à 1,79
1,80 à 1,84
1,85 à 1,89
1,90 à 1,94
Total
Effectif
16
151
Fréquence
10,6 %
100 %
b. Donner les résultats de ce tableau en effectifs cumulés croissants (T est la Taille):
Taille
T  1,69
T  1,74
T  1,79
T  1,84
T  1,89
T  1,94
Effectif cumulé croissant
16
151
Fréquence cumulée croissante (%)
10,6 %
100 %
c. Donner les résultats de ce tableau en effectifs cumulés décroissants (T est la Taille):
Taille
1,65  T
1,70  T
1,75  T
1,80  T
1,85  T
1,90  T
Effectif cumulé décroissant
151
5
Fréquence cumulée décroissante (%)
100 %
3,3 %
Âge (caractère)
14
15
16
17
TOTAL
Effectif
1
27
5
2
35
Effectif cumulé croissant
1
28
33
35
Effectif cumulé décroissant
35
34
7
2
Fréquence (%)
0,029 (2,9)
0,771 (77,1)
0,143 (14,3)
0,057 (5,7)
1 (100)

3
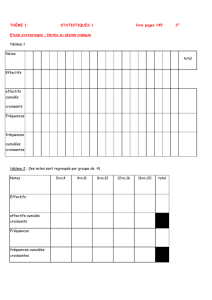
EXERCICE 2 :
Une étude statistique a été effectuée sur les élèves de 2de d’un lycée. Le caractère étudié est leur moyenne annuelle
en Mathématiques. Pour chaque note, on a indiqué le nombre de personnes correspondant.
TABLEAU 1
Note (/20)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Total
Effectif
0
1
0
5
6
2
11
7
23
25
30
16
26
15
19
14
11
5
2
3
0
221
a. Compléter le tableau :
TABLEAU 2
Note (/20)
0  N < 4
4  N < 8
8  N < 12
12  N < 16
16  N  20
Effectif
Effectif cumulé croissant
Effectif cumulé décroissant
Fréquence cumulée croissante (%)
Fréquence cumulée décroissante (%)
2. Etude d’une série statistique : caractère quantitatif discret
Utilisons trois exemples pour traiter cette partie :
1) Voici les notes de Julie en Maths.
Note (xi)
9
10
11
12
13
14
15
Effectif (ni)
1
2
1
2
1
1
1
2) Voici les notes de Jérôme en maths : 4 ; 6 ; 18 ; 7 ; 17 ; 12 ; 12 ; 18.
3) Voici les notes de Bertrand en maths : 13 ; 13 ; 12 ; 10 ; 12 ; 3 ; 14 ; 12 ; 14 ; 15.
a. Représentation graphique
On utilise un nuage de points (les effectifs sont représentés par l’axe des ordonnées et l’axe des abscisses
représente le caractère étudié)

4
On peut aussi utiliser un diagramme en bâtons ou un diagramme circulaire.
Exercice 2 (suite) :
b. Construire le diagramme en bâtons des effectifs du
TABLEAU 1.
c. Construire l’histogramme des effectifs du TABLEAU 2.
b. Caractéristiques de position
Les indicateurs de position proposent une tendance centrale de la série.
 Mode :
Le(s) mode(s) est(sont) la(les) valeurs du caractère pour laquelle l’effectif est le plus grand.
Exemple : Le mode de la série statistique des notes de Julie sont les notes 10 et 12.
0
1
3
4
2
5
6
7
9
10
8
11
12
13
15
14
16
17
18
20
19
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
0
1
3
4
2
5
6
7
9
10
8
11
12
13
15
14
16
17
18
20
19
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150

5
 Moyenne :
Technique :
 La série statistique est une liste de valeurs :
 La moyenne est la somme de toutes ces valeurs divisée par le nombre de valeurs.
 La série statistique est donnée sous forme de tableau :
 On connait les effectifs.
La moyenne est la somme des produits divisée par l’effectif total. Elle est souvent notée .
 On connait les fréquences :
Exemple :
Moyenne des notes de Jérôme :
4 6 18 7 17 12 12 18 11,75
8
Moyenne des notes de Bertrand :
13 13 12 10 12 3 14 12 14 15 11,8
10
Moyenne des notes de Julie :
9 10 2 11 12 2 13 14 15 11,8
9
        ;
.
EXERCICE 3 :
Un élève a obtenu les notes suivantes en mathématiques :Ecrit : 12 ; 15 ; 9 ; 18 ; 11 et Oral : 8 ; 7 ; 0 ; 11
a. Calculer la moyenne de l’écrit et la moyenne de l’oral
b. Calculer la moyenne générale de l’élève sachant que l’écrit compte 4 fois plus que l’oral.
EXERCICE 4 :
Dans une équipe de foot il y a :
- 3 gardiens de but dont la taille moyenne est 1,91m
- 8 défenseurs dont la taille moyenne est 1,84m
- 7 milieux de terrains dont la taille moyenne est 1,79m
- 4 attaquants dont la taille moyenne est 1,81m
Calculer la taille moyenne des joueurs de l’équipe (On arrondira au centimètre).
EXERCICE 5 :
Ce tableau récapitule le salaire brut annuel moyen en fonction de la catégorie socioprofessionnelle et du sexe en
2001 :
Statut
Ensemble
Hommes
Femmes
Part des effectifs
hommes
Part des effectifs
femmes
Cadre
40 520
43 140
32 930
19,0 %
12,5 %
Profession intermédiaire
21 300
22 510
19 440
22,3 %
27,6 %
Employé
15 200
16 080
14 790
10,8 %
43,9 %
Ouvrier
15 340
15 750
b.
48,0 %
16,0 %
Moyenne
20 960
a.
18 050
--
--