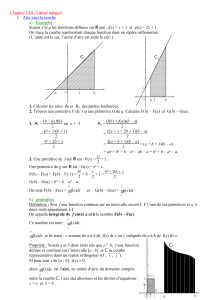
Chapitre 10 TS 2 Intégration On considère un repère orthogonal . 1

Chapitre 10 TS 2
1
Intégration
On considère un repère orthogonal
jiO ,;
.
1 unité d’aire (u.a.) est l’aire du rectangle OIKJ.
I – Intégrale d’une fonction positive
Définition :
On considère une fonction f continue et positive sur
ba;
.
f
C
est sa courbe représentative
dans le repère
jiO ,;
.
On définit le domaine D délimité par :
f
C
,
 Les droites d’équation
ax
et
bx 
,
 L’axe des abscisses.
L’aire de D, exprimée en unités d’aire, est le réel
b
a
dxxf )(
. Cette écriture ce lit « somme (ou
intégrale) de a à b de
dxxf )(
». a et b sont les bornes de l’intervalle.

Chapitre 10 TS 2
2
Remarque :
Dans l’écriture
b
a
dxxf )(
, la variable x n’a aucune signification particulière : on pourrait
l’appeler autrement :
b
a
duuf )(
ou
b
a
df )(
(il s’agit d’une variable muette).
Exemples :
 Si
ba 
alors
0)( 
b
a
dxxf
.
 Si
0)(  mxf
alors
mabdxxf
b
a
)()( 
.
Définition :
Soit f une fonction continue et positive sur
ba;
. La valeur moyenne de f sur
ba;
est
b
a
dxxf
ab )(.
1
.
Remarques :
b
a
dxxf
ab
m)(.
1
équivaut à
b
a
dxxfmab )()(
. Autrement dit, la valeur
moyenne est telle que l’aire du rectangle de dimensions
ab
et m est égale à celle
« sous la courbe de f ».
 En cinématique, m, la vitesse moyenne est la vitesse constante nécessaire pour
parcourir la même distance entre les temps a et b.
 En physique, si
)(xfy 
alors
b
a
dxxf )(
est une grandeur homogène à
xy
et
b
a
dxxf
ab )(.
1
est une grandeur homogène à y.

Chapitre 10 TS 2
3
II – Intégrale d’une fonction de signe quelconque
1) Intégrale d’une fonction négative
Définition :
On considère une fonction f continue et négative sur
ba;
.
On définit l’intégrale de a à b de f par
Adxxf
b
a
)(
où A est l’aire du domaine D du plan
délimité par la courbe
f
C
, les droites d’équation
ax 
et
bx 
et l’axe des abscisses.
Exemple :
Soit f définie sur par
2
2
1
)(  xxf
.
f est continue et négative sur
4;0
.
Alors
4
224
edu triangl aire 2
2
1
)( 4
0
4
0
  OABdxxdxxf
.
2) Cas général
On considère une fonction f continue sur
ba;
.

Chapitre 10 TS 2
4
1
A
est la réunion de toutes les parties du plan délimitées par
f
C
, les droites d’équation
ax
et
bx 
et l’axe des abscisses, et au-dessus de cet axe.
2
A
: idem mais sous l’axe des abscisses.
On pose
21 de aire de aire )( AAdxxf
b
a
.
Exemple (suite) :
341 de aire de aire )(
6
0
AOBBDCdxxf
.
Définition :
Soit f une fonction continue sur
ba;
. La valeur moyenne de f sur
ba;
est
b
a
dxxf
ab )(.
1
.
Exemple (suite) :
Valeur moyenne de f sur
6;0
:
2
1
6
3
)(.
06 16
0
dxxf
.
III – Primitives d’une fonction
Définition :
Soit f une fonction définie sur un intervalle I.
On appelle primitive de f sur I toute fonction F définie sur I telle que
fF '
.

Chapitre 10 TS 2
5
Autrement dit :
Remarque :
On admet que si f est continue sur I alors f admet des primitives sur I.
Exemples :
Les fonctions
7
3
3
x
x
et
4
3
3
x
x
définies sur sont des primitives de la fonction
²xx
définie sur .
En effet,
'
3
'
34
3
²7
3
x
x
x
.
Théorème : Preuve 1
Soit f une fonction définie sur un intervalle I qui admet une primitive de f sur I.
 Les primitives de f sur I sont les fonctions G de la forme
kF 
, k réel fixé, définies
sur I. Autrement dit : deux primitives sur I d’une même fonction diffèrent d’une
constante.
 Pour tous couples de réels
00 ;yx
, il existe une unique primitive
0
F
de f sur I telle
que
000 )( yxF 
.
Interprétation graphique :
Les courbes des primitives de f sur I sont les images de celle de F par des translations de
vecteur
jk
.
Par un point quelconque
000 ;M yx
, il passe une seule courbe d’une primitive de f sur I.