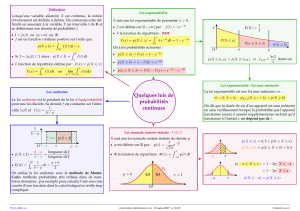
Introduction à la loi normale

Introduction à la loi normale 1/2
Introduction à la loi normale
Activité 1 : pourquoi centrer et réduire ?
1. Une entreprise commercialise des poulets. Les masses des poulets de la production ont pour
moyenne
1500m
g et pour écart-type 200 g.
On choisit un poulet au hasard dans la production.
Sa masse en gramme est une variable aléatoire
1
X
vérifiant
1
( ) 1500EX 
et
1
( ) 200X
.
a) Un poulet a pour masse
x
1600.
Calculer sa masse centrée
xm
et sa masse centrée réduite
xm
.
b) La variable aléatoire
1
1Xm
Z
est appelée variable centrée réduite associée à
1
X
.
Déterminer l’espérance et l’écart-type de la variable aléatoire
1
Z
.
Pour une variable X et a, b réels, on donne les relations :
( ) ( )E aX b aE X b  
et
2
( ) ( )V aX b a V X
.
2. Comparaison
Un autre producteur commercialise des poulets dont les masses ont pour moyenne 1650 g et
pour écart-type 150 g. La masse en gramme
2
X
d’un poulet pris au hasard dans cette production
vérifie
2
( ) 1650EX 
et
2
( ) 150X
.
a) Exprimer la masse centrée réduite
2
Z
en fonction de
2
X
.
b) On admet que
1
Z
et
2
Z
suivent la même loi de probabilité.
Une personne achète un poulet au hasard dans chaque entreprise.
A-t-elle plus de chance d’avoir un poulet de plus de 1600 g de la première entreprise qu’un
poulet de plus de 1750 g de la seconde entreprise » ?
Activité 2 : vers le théorème de Moivre Laplace

Introduction à la loi normale 2/2
Sur ce graphique, on a représenté les diagrammes en bâtons d’une variable X suivant la loi
binomiale b (n, p) et ceux des variables
Y X np
et
(1 )
X np
Znp p
(centrée réduite associée).
On remarque que pour les « grandes binomiales » le diagramme de Z a toujours à peu près la même
allure : celle d’une courbe en cloche, symétrique par rapport à (Oy).
1. Si X suit la loi binomiale b (n, p), démontrer que la variable centrée réduite associée vérifie
( ) 0EZ 
et
( ) 1VZ
.
2. Cas particulier :
100n
et
0,4p
.
a) Justifier que Z prend les valeurs
40
24
kk
z
, pour tout entier k tel que
0 100k
.
b) Quel est l’écart entre deux valeurs consécutives
k
z
et
1k
z
?
c) On désire représenter la variable Z par un histogramme d’aire totale égale à 1 (comme une
loi à densité). Chaque rectangle a pour centre
k
z
, pour largeur
11
24
, et pour aire
()
k
P Z z
. Montrer que la hauteur de ce rectangle est
( ) 24P X k
.
3. Cas général : n et p sont quelconques.
a) Justifier que Z prend les valeurs
(1 )
kk np
znp p
, pour tout entier k tel que
0kn
.
b) Quel est l’écart entre deux valeurs consécutives
k
z
et
1k
z
?
c) On désire représenter la variable Z par un histogramme d’aire totale égale à 1 (comme une
loi à densité). Chaque rectangle a pour centre
k
z
, pour largeur
11
(1 )np p
, et pour aire
()
k
P Z z
. Montrer que la hauteur de ce rectangle est
( ) (1 )P X k np p  
.
Avec Geogebra
Créer successivement :
un curseur n allant de 10 à 1000
un curseur p allant de 0 à 1
Les nombres
m np
et
(1 )s np p
Abscisse = Séquence[(
()km
/s, k, 0, n]
Proba = Séquence[Combinaison[n, k] p^k (
1p
)^(
nk
), k, 0, n]
OU
Proba= Séquence[Binomiale[n,p,false], k, 0, n]
H= Barres[Abscisse, Proba*s]
Faire varier n et p. Que peut-on observer ?
On introduit la fonction
2
2
1
:e
2π
x
fx 
.
Représenter f sur la même figure que l’histogramme.