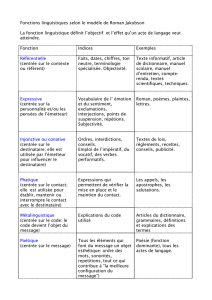
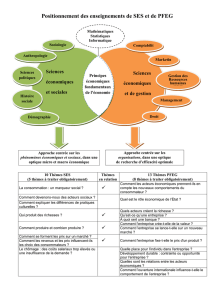
ECS 2 Statistiques univariées (Cas discret) TP 5

ECS 2 Statistiques univariées (Cas discret) TP 5
à faire en classe par le groupe 1
Pour les exercices qui suivent, on sera amené à utiliser une table de la fonction de répartition de la loi normale centrée réduite
dont voici un extrait :
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
1,2
0,8849
0,8869
0,8888
0,8907
0,8925
0,8944
0,8962
0,8980
0,8997
0,9015
1,6
0,9452
0,9463
0,9474
0,9484
0,9495
0,9505
0,9515
0,9525
0,9535
0,9545
Exercice 1 :
On définit une série statistique par l’instruction suivante : X=floor( grand(1,100,’‘nor’’,2,2))
1. Quelles sont les valeurs possibles de X ? Quel est l’intérêt de « floor » ?
2. Quel est l’effectif total de la série statistique ?
3. Représenter la série statistique à l’aide de la commande « bar ». Quel est le mode ?
4. R=gsort(X,’g’,’i’) affecte à R la série statistique ordonnée dans le sens croissant dont les éléments sont ceux de
X. Représenter R à l’aide de la fonction « bar ». Evaluer à partir de ce graphique les trois quartiles et le mode.
5. Affecter à T la matrice des modalités croissantes-effectifs de la série statistique X. Concaténer T avec la colonne
des fréquences cumulées. Retrouver alors les valeurs des quartiles et du mode.
6. Déclarer une fonction Scilab qui à une série statistique X associe la matrice formée de son ou ses modes.
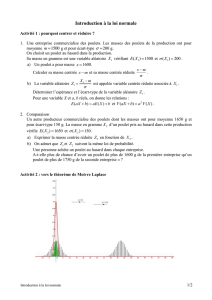
7. Par le calcul Scilab, retrouver les valeurs du ( ou des )mode(s) et des quartiles de la série statistique X et calculer
sa moyenne et son écart-type n-1
8. Un peu de probabilités : Soit Z une variable aléatoire de loi normale N(2,4).
On note Z* la variable aléatoire centrée réduite associée. Rappeler la relation entre Z et Z*.
Avec la table de la fonction de répartition de la loi normale centrée réduite, donner un réel m tel que
P[ |Z*| ≤ m ]  0,9. En déduire deux entiers a et b tels que P[ a ≤ ⌊ Z ⌋ ≤ b ]  0,9
9. A l’aide de la fonction « dsearch », calculer le nombre de valeurs de X comprises entre a et b. Conclure.
Exercice 2 :
1. Remplacer les points par ce qu’il faut pour que l’instruction : X = grand(1,100, ... , ... , ... ) simule une série
statistique de 100 termes X(1) , ... , X(100) où X(i) est le nombre de pile obtenus au cours de 10 jets d’une
pièce équilibrée.
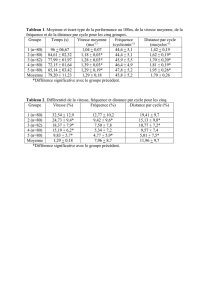
2. Calculer la moyenne et l’écart-type empirique de la série X.
Ces résultats sont-ils conformes à vos prévisions ? Proposer un moyen d’obtenir de meilleures valeurs.
3. Représenter cette série à l’aide d’un diagramme circulaire avec légendes.
4. Lire le mode sur ce graphique.
5. Représenter sur une autre feuille graphique, le diagramme en bâtons des fréquences cumulées. Lire la
médiane sur ce graphique.
6. Rappeler la formule de Koenig-Huygens.
Compléter la fonction suivante pour qu’elle calcule la variance ( au sens des probabilités ) de X :
function V=Var(X) // X est un vecteur-ligne
n = length(X)
V=X*X’
……
Endfunction
Appliquer cette fonction à la série statistique X et comparer l’écart-type empirique à l’écart-type.

NOM Statistiques univariées (Cas discret) TP 5
à faire à la maison par le groupe 2
Pour les exercices qui suivent, on sera amené à utiliser une table de la fonction de répartition de la loi normale centrée réduite dont voici un
extrait :
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
1,2
0,8849
0,8869
0,8888
0,8907
0,8925
0,8944
0,8962
0,8980
0,8997
0,9015
1,6
0,9452
0,9463
0,9474
0,9484
0,9495
0,9505
0,9515
0,9525
0,9535
0,9545
Exercice 1 :
On définit une série statistique par l’instruction suivante : X=floor( grand(1,100,’’nor’’,2,2))
1. Quelles sont les valeurs possibles de X ? Quel est l’intérêt de « floor » ?
2. Quel est l’effectif total de la série statistique ?
3. Ecrire les instructions permettant de représenter le diagramme en bâtons exploitable de cette statistique.
4. R=gsort(X,’g’,’i’) affecte à R la série statistique ordonnée dans le sens croissant dont les éléments sont ceux de X.
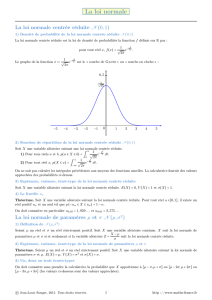
L’instruction bar(R) donne le graphique suivant :
Evaluer à partir de ce graphique les trois quartiles et le mode.
5. Déclarer une fonction Scilab qui à une série statistique brute X associe
la matrice formée de son ou ses modes.
6. Un peu de probabilités : Soit Z une variable aléatoire de loi normale
N(2,4). On note Z* la variable aléatoire centrée réduite associée.
Rappeler la relation entre Z et Z*.
A l’aide de la table de la fonction de répartition de la loi normale
centrée réduite, déterminer un réel m tel que P[ |Z*| ≤ m ]  0,9
En déduire deux entier a et b tels que P[ a ≤ ⌊ Z ⌋ ≤ b ]  0,9
7. A l’aide de la fonction « dsearch », calculer le nombre de valeurs de X
comprises entre a et b. Que devrait-on obtenir ?
Exercice 2 :
1. Remplacer les points par ce qu’il faut pour que l’instruction : X = grand(1,100, ... , ... , ... ) simule une série statistique de
100 termes X(1) , ... , X(100) où X(i) est le nombre de pile obtenus au cours de 10 jets d’une pièce équilibrée.
2. Ecrire les instructions Scilab permettant le calcul e la moyenne et d’une valeur approchée de l’écart-type de la série X.
Quels résultats devrait-on observer ?
3. Ecrire les instructions permettant de représenter cette série à l’aide d’un diagramme circulaire avec légendes.
Voilà ce que l’on obtient : --------------------------------->
Lire le mode sur ce graphique.
5. Ecrire les instructions permettant de représenter sur
une autre feuille graphique, le diagramme en bâtons
des fréquences cumulées.
Voilà ce que l’on obtient :
<-----> Lire la médiane sur ce graphique.
6. Rappeler la formule de Koenig-Huygens.
Compléter la fonction suivante pour qu’elle calcule la variance ( au sens des probabilités ) de X :
function V=Var(X) // X est un vecteur-ligne
n = length(X); V=X*X’
……
endfunction