TP TS 14 Mouvement des satellites et planètes. But : Vérifier les trois

TP TS 14 Mouvement des satellites et planètes.
But :
Vérifier les trois lois de Kepler sur un exemple : le mouvement de Mercure autour du Soleil
Etudier le cas particulier de la trajectoire circulaire d’un satellite de la Terre.
1. Le mouvement de Mercure.
L’orbite d’une planète désigne la trajectoire de son centre d’inertie dans un référentiel héliocentrique, lors de son
mouvement autour du Soleil. La période sidérale ou orbitale, c'est-à-dire la durée d’une révolution, est égale au
temps mis par la planète pour décrire toute son orbite.
Le doc. 1 reproduit le mouvement de Mercure au cours d'une révolution dans un référentiel héliocentrique, le point
S désignant le centre du Soleil. La période orbitale T est de 87,97 jours. Les positions de Mercure sont séparées
d'une durée égale à
30
T
. Les axes sont gradués en millions de km. (Voir doc.1 agrandi en annexe)
Doc. 1. Graphique illustrant le mouvement de Mercure. Doc. 2. Orbite circulaire et elliptique d'une planète.
1.1. Paramètres d’une ellipse.
C’est en exploitant les résultats de mesures astronomiques que Johannes Kepler a prouvé, au début des années
1600, le caractère elliptique de l’orbite de Mars. Bien qu’un cercle centré sur le Soleil soit une orbite théoriquement
possible pour une planète, toutes les planètes du système solaire ont des orbites elliptiques.
Un cercle est caractérisé par le plan dans lequel il est contenu. Ses points sont à une distance constante du centre C.
Une ellipse est également caractérisée par le plan qui la contient; on peut la définir comme l'ensemble des points M,
dont la somme des distances MF1 + MF2 à deux points fixes F1 et F2 est constante. Kepler appela ces deux points
particuliers les foyers de l'ellipse (voir doc. 2).
Pour les orbites planétaires, le centre S du Soleil est l’un des foyers. Le point S est excentré : il n’est pas au centre C
de l’ellipse. L'axe passant par les points C et S est appelé le grand axe de l'ellipse. Sa longueur est notée 2a.
L'aphélie A et le périhélie P désignent les positions de la planète lorsque l’éloignement au Soleil est respectivement
maximum ou minimum : on a donc AP = 2a. Le diamètre du cercle de centre C et passant par les points A et P est
égal à 2a : l'ellipse est située à l'intérieur de ce cercle.
1.2. Première loi de Kepler.
Dans le référentiel héliocentrique, les trajectoires des planètes du système solaire sont des ellipses dont le soleil
occupe l’un des foyers
Tout point M d’une ellipse vérifie l’égalité MF1 + MF2 = 2a (*)
 Sur le document 1 agrandi, indiquer A, P. Noter C le centre de l’ellipse. En déduire F2.
 Vérifier l’égalité (*) pour deux points quelconques de la trajectoire de mercure autour du Soleil.
Conclure quant à la nature elliptique de la trajectoire de Mercure.

1.3. Deuxième loi de Kepler.
Le segment [SM] qui relie le centre du Soleil à celui de la planète balaie des aires égales pendant des durées
égales.
On considère sur le doc. 1 l'aire A2 de la surface limitée par les rayons SM1, SM3 et par la portion M1M3 de la
trajectoire. On définit également les aires A9 et A17 correspondant aux surfaces limitées par les rayons SM8 et
SM10 pour l'une, et SM16 et SM18 pour l'autre.
 Qu’implique la deuxième loi de Kepler pour les valeurs de A2, A9 et A17 ?
 Nécessairement la vitesse de Mercure n’est pas uniforme sur son orbite. En quel point est-elle maximale ?
minimale ?
1.4. Troisième loi de Kepler.
Le carré de la période de révolution T d’une planète est proportionnel au cube de la longueur a du demi-grand axe
de son orbite :
k
a
T
3
2
(k est une constante).
Simulation
Les lois de Kepler s’appliquent aux mouvements des planètes autour du Soleil comme aux mouvements d’un
satellite autour d’une planète
 Ouvrir le logiciel Hatier TS puis obligatoire > simulateurs > satellite TS
 Pour une prise en main lire le texte introductif et faire l’exercice « prise en main »
 Dans affichage cocher : tracer la trajectoire et afficher le vecteur vitesse
 Dans conditions initiales choisir successivement trois conditions initiales du tableau ci-dessous ; (position : 0°
et angle avec le rayon : 90° )
 Pour chaque cas mesurer la période de révolution à l’aide du chronomètre (ne pas se placer dans Plan
orbital ; faire plusieurs mesures) ainsi que les altitudes au périgée hP et à l’apogée hA. Changer la couleur de
chaque trajectoire
v0 (m/s)
h0 (km)
hA (km)
hP (km)
2 a (km)
a (m)
T
(j,h,min,s)
T (s)
T2 / a3
(s2.m-3)
2500
40000
3500
35000
4000
30000
T2 / a3 est-il constant ?
2. Cas du mouvement circulaire uniforme : mouvement d’un satellite géostationnaire.
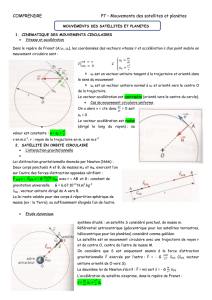
2.1. Vecteur vitesse et vecteur accélération
Dans le logiciel choisir les conditions initiales suivantes : h0 = 35794 km, v0 = 3085 m.s-1, angle : 270°, position : 0°
Afficher le vecteur vitesse et afficher le vecteur accélération.
 Représenter la terre, le satellite et sa trajectoire ainsi que les vecteurs vitesse
v
et accélération
a
.
Les vecteurs sont-ils constants ?
Leurs normes sont-elles constantes ?
Que peut-on dire de
v
.
a
?

 Calculer
r
v2
avec r= h + RT et le comparer à a mesuré à l’écran. Conclure. ( RT = 6380 km)
 Mesurer la période de révolution T et la comparer à la période de rotation propre TT de la Terre (jour
sidéral) TT = 86164 s ; conclure.
 Donner une définition du satellite géostationnaire, sachant qu’il doit obéir aux contraintes supplémentaires
suivantes :
- le plan de l’orbite est le plan équatorial ;
- la trajectoire est décrite dans le même sens que le sens de rotation de la Terre (condition respectée
avec un angle avec le rayon de 270°)
2.2. Application de la deuxième loi de Newton
 Quelle est la force qui s’exerce sur le satellite ?
Donner ses caractéristiques.
 En appliquant la deuxième loi de Newton au satellite,
dans le référentiel géocentrique considéré comme
galiléen, montrer que
3
2
T
R
T
=
T
GM
2
4
où MT est la masse de la Terre
 en déduire MT.
Donnée :
constante de gravitation universelle : G = 6,67.10-11S.I.