Dérivation de fonction

D:\769801674.doc
Dérivation et étude de fonctions
Objectifs :
Etre capable de
 Définir le nombre dérivé et calculer une fonction dérivée
 Etudier une fonction à l’aide de la fonction dérivée
 Construire la tangente en un point de la courbe
Activité 1 :Découverte sur la tangente et le nombre dérivé
Activité 2 :Dérivée de fonction usuelle et tangente
Activité 3 : Signe de la dérivée et sens de variation
Activité 4 : Etude de la fonction f(x)=x3-3x²+2
Activité 5 :Bilan

D:\769801674.doc
Activité 1
Soit la représentation graphique de la fonction f(x)=x²
On trace la tangente en ce point à la courbe .Trouver l’équation des droites et relever la valeur de leur coefficient
directeur (voir feuille rappel)
Remplir le tableau ci dessous
Abscisse du point
Coefficient directeur de la
tangente
F’(x)
Appelons f’(x) la fonction 2x
Comparer pour les différentes valeur de x la valeur de f’(x) et du coefficient directeur de la droite.
On dit que f’(x)=2x est la dérivée de f(x)=x²

D:\769801674.doc
RAPPEL
1. RAPPEL
Trouver l'équation de la droite (AB) du type y = ax + b
passant par les points A(3 ; -5) et B(-2 ; 5).
1.1. Par le calcul.
 Calcul du coefficient directeur a de la droite (AB) :
a =
Error!
=
 Calcul du coefficient b (ordonnée à l'origine) :
b = y – ax =
1.2. Graphiquement.
a =
Error!
=
b =
d'où l'équation de la droite (AB) est y =
-3
-2
-1
0
1
2
3
x
5
4
3
2
1
-1
-2
-3
-4
-5
-6
y
y
i
j
B
A
y
x
b

D:\769801674.doc
Activité 2
 Définition :
On dit qu’une fonction f est dérivable sur un intervalle I, lorsqu’elle est dérivable pour tout nombre réel x0 de I
 Tableau de dérivée de fonction usuelle
Fonctions
Dérivée
a
0
x
1
ax
a
x²
2x
x3
3x²
1
x
-
1
x²
Opération
Dérivée
Somme : u+v
u’+v’
Produit par un réel k : ku
ku’
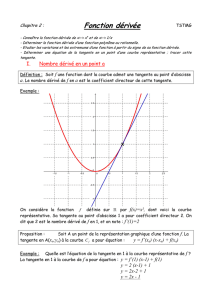
 Equation de la tangente à une courbe
La tangente à une courbe a pour équation
Y= f’(x0).(x-x0)+f(x0)
Exemple :
Soit la fonction définie par f(x)=x²-2x+1
Trouver et tracer f(x) ;f’(x) ;l’équation de la tangente au point x=2
Quel est la position de la tangente par rapport a la courbe ?

D:\769801674.doc