Division euclidienne - Collège Les Grands Champs

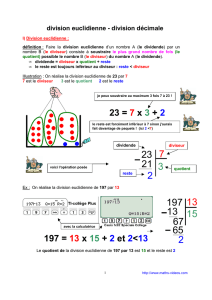
dividende
quotient
reste
diviseur
6ème Chapitre 5 : La division
I - Division euclidienne
Définition : Effectuer une division euclidienne, c’est trouver deux nombres entiers : le quotient et le
reste.
Exemple :
762 = 12
63 + 6
Propriété : On a :
dividende = diviseur quotient + reste
Le reste est toujours strictement inférieur au diviseur.
Dans une division euclidienne, le quotient, le dividende, le diviseur et le reste sont
toujours des nombres entiers.
On ne peut pas diviser pas zéro.
II - Diviseurs et multiples
1) Définition
Définition : Si le reste de la division euclidienne d’un nombre entier a par un nombre entier b est égal à
zéro, on dit que ce nombre a est divisible par b.
ou b est un diviseur de a
ou a est un multiple de b.
Exemple :
Le reste de la division euclidienne de 91 par 13 est 0 donc on dit :
91 est divisible par 13.
ou 13 est un diviseur de 91.
ou 91 est un multiple de 13.
2) Critères de divisibilité :
 Un nombre entier est divisible par 2 si son chiffre des unités est 0, 2, 4 ,6 ou 8.
 Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5.
 Un nombre entier est divisible par 3 si la somme de ses chiffres est divisible par 3.
 Un nombre entier est divisible par 9 si la somme de ses chiffres est divisible par 9.
Exemple : 1 248 est-il divisible par 3, par 9 ?
On a : 1+2+4+8 = 15 et 15 est divisible par 3 mais pas par 9
Donc 1 248 est divisible par 3 mais n’est pas divisible par 9.
7
6
2
1
2
7
2
6
3
4
2
3
6
6
9
1
1
3
9
1
7
0

III – Division décimale
1) Dividende entier et diviseur entier
Quel est le nombre qui multiplié par 5 donne 18 ?
5 = 18
Réponse :
Ce nombre est le quotient de 18 par 5.
 = 18 ÷ 5
 = 3,6 (C’est l’écriture décimale de 18 ÷ 5.)
2) Dividende décimal et diviseur entier
Quel est le nombre qui multiplié par 5 donne 43,5 ?
5 = 43,6
Réponse :
Ce nombre est le quotient de 43,5 par 5.
 = 43,5 ÷ 5
 = 8,7 (C’est l’écriture décimale de 43,5 ÷5)
Méthode : Dès que l’on abaisse le premier chiffre après la virgule du dividende, on place la virgule au
quotient.
3) Lorsque le diviseur est un nombre décimal
Propriété : On ne change pas le quotient de deux décimaux quand on multiplie chacun d’eux par un même
nombre ( en particulier 10 ; 100 ; 1000…).
Cette propriété permet de transformer une division lorsque le diviseur est un nombre décimale.
Exemple 1 : Calculer le quotient de 29,4 par 1,4.
Réponse : On multiplie le dividende et le diviseur par 10. Cela revient à calculer le quotient de
294 par 14. On trouve le nombre 18,5.
Exemple 2 : Calculer le quotient de 2 par 0,25
Réponse : On multiplie le dividende et le diviseur par 100. Cela revient à calculer le quotient de
200 par 25. On trouve le nombre 8.
1
8,
0
5
1
5
3,
6
3
0
3
0
0
4
3,
5
5
4
0
8,
7
3
5
3
5
0
En 18 combien de fois 5 ? 3 fois, 3 fois 5 égal 15 ôté de 18 reste 3 unités à partager. 3 unités sont égales à 30
dixièmes que l’on partage en 5 parties de 6 dixièmes.
Le quotient de 18 par 5 est donc égal à 3 unités 6 dixièmes = 3,6
En 43 combien de fois 5 ? 3 fois, 8 fois 5 égal 40 ôté de 43 reste 3 unités et 5 dixièmes à partager. 3 unités et
5 dixièmes sont égales à 35 dixièmes que l’on partage en 5 parties de 7 dixièmes.
Le quotient de 43,5 par 5 est donc égal à 8 unités 7 dixièmes = 8,7

IV - Troncature et arrondis à l’unité
Problème : Loïc désire partager une planche de140 cm en trois planches de longueurs égales. Quelle sera
la longueur de chaque planche ?
On a un souci : la division ne s’arrête pas !!
On trouve :
140 : 3 = 46,666666666…
Définition : Dans ce cas on donne une valeur approchée.
 La troncature à l’unité d’un nombre est sa partie entière.
 L’arrondi à l’unité d’un nombre est le nombre entier le plus proche.
Exemple 1 : Dans le problème
La troncature à l’unité du quotient de 140 par 3 est 46
L’arrondi à l’unité du quotient est 47.
Exemple 2 :
103,85
7,263
12,5
Troncature à l’unité
103
7
12
Arrondi à l’unité
104
7
13
1
4
0,
0
3
1
2
4
6,
6
2
0
1
8
2
0
1
8
2