1. Division euclidienne 2. Diviseurs et multiples

6ème Cours division et problèmes
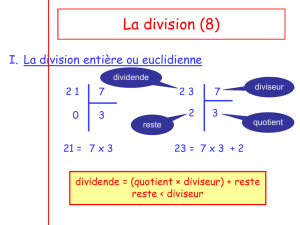
1. Division euclidienne
Effectuer une division euclidienne c’est trouver deux nombres entiers : le quotient et le reste.
Exemple : 1 273 15
73 84
13
1 273 = 15 x 84 + 13
Dividende = diviseur x quotient + reste
Le reste est toujours inférieur au diviseur
Attention :
Dans une division euclidienne, le quotient, le dividende et le reste sont toujours des
nombres entiers.
On ne peut pas diviser par 0
Contrôler le résultat d’une division euclidienne
On vérifie que le reste est inférieur au quotient
On vérifie qu’ on retrouve le dividende si on multiplie le quotient par le diviseur et
qu’on ajoute le reste.
2. Diviseurs et multiples
a) Définition
Si le reste de la division euclidienne d’un entier a par un entier b est zéro, on dit :
a est divisible par b
ou b est un diviseur de a
ou a est un multiple de b.
Exemple : Le reste de la division de 128 par 8 est 0.
On dit donc :
128 divisible par 8
8 est un diviseur de 128
128 est un multiple de 8
b) critères de divisibilité
1
dividende
reste
quotient
diviseur

6ème Cours division et problèmes
Un nombre entier est divisible par 2 si son chiffre des unités est 0,2, 4, 6 ou 8.
Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5.
Un nombre entier est divisible par 3 si la somme de ses chiffres est divisible par 3.
Un nombre entier est divisible par 9 si la somme de ses chiffres est divisible par 9.
Exemples :
2 184 est divisible par 3 car 2 + 1 + 8 + 4 = 15 et 15 est divisible par 3
72 648 est divisible par 9 car 7 + 2 + 6 + 4 + 8 = 27 et 27 est divisible par 9.
3. Division décimale
a) Définition
b x = a (b
)0
Ce nombre qui est appelé quotient de a par b est le résultat de la division décimale de a par b.
Il est noté a
b
ou
b
a
b) Exemple
84 x 2,5 = 210
On écrit 2,5 = 210 84 ou 2,5 =
84
210
Attention !
Le quotient de deux nombres décimaux n’est pas toujours un nombre décimal.
Exemple : 87 11 n’est pas un nombre décimal car la division ne se termine pas.
c) Propriété
On ne change pas le quotient de deux nombres si on multiplie ces deux nombres par un même
nombre non nul, en particulier par 10, 100, 1 000, etc…
Cette propriété permet de transformer la division de deux nombres « à virgule » en une
division de deux nombres entiers.
Exemple : 15,3 2,17 = 1 530 217
d) Division par 0,1 ; 0,01 ; 0,001 ; etc …
2
2,5 est le quotient de la division
décimale de 210 par 84

6ème Cours division et problèmes
Diviser un nombre par 0,1 ou 0,01 ou 0,001 revient à le multiplier par 10 ou 100 ou 1000.
Diviser un nombre décimal par 0,1 ou 0,01 ou 0,001 revient à décaler la virgule de ce nombre
de 1 ou 2 ou 3 rangs vers la droite.
Exemples :
5,14 0,1 = 51,4 5,273 0,01 = 524,3 67 0,001 = 67 000
4. Troncatures et arrondis à l’unité
Troncature La troncature à l’unité de
3,42 est 3
La troncature à l’unité de
3,62 est 3
Arrondi L’arrondi à l’unité de 3,42
est 3 (car 4 < 5)
L’arrondi à l’unité de 3,62 est
4 (car 6 > 5)
L’arrondi à l’unité d’un nombre est l’entier le plus proche de ce nombre.
3