3 Propriétés des fonctions continues sur un intervalle

CONTINUITE DES FONCTIONS
REELLES D’UNE VARIABLE
REELLE

1
On appelle fonction réelle d’une variable réelle une fonction d’une partie de R à valeurs dans R.
1 LIMITE D’UNE FONCTION REELLE
1.1 DEFINITIONS
1 - Soit A une partie de R et un point a  R, a est adhérant à A si et seulement si   > 0, [a-, a+]  A  
L’ensemble des points adhérant à A est appelé l’adhérence de E et est noté /A.
2 - Soit f : A  R, a  /A, on dit que le nombre l  R est limite de f lorsque x tend vers a si et seulement si :
  >0,  >0 tel que (x  A et | x – a |<) => |f(x) – l |< .
1.2 REMARQUE
a n’appartient pas forcément à A.
Si B est une partie de A et si la restriction de f à B admet une limite l lorsque x tend vers a, on écrit :
lim xa xB f(x)=l
1.3 DEFINITIONS
Soient A une partie non majorée de R, (respectivement non minorée) et f : A  R, on dit :
1) f tend vers +¤¤ lorsque x tend vers +¤¤ par valeurs dans A si et seulement :
 M >0,  k >0 tel que (x>K et x  A => f(x)>M)
2) respectivement :
f tend vers +¤¤ lorsque x tend vers -¤¤ par valeurs dans A si et seulement si :
 M>0,  K’ < 0 tel que (x<K’ et x  A => f(x) >M)
1.4 PROPOSITIONS
Soient f :AR, a  A, l  R alors f admet l pour limite lorsque x tend vers a si et seulement si pour toute suite
(xn)n1 de points de A qui converge vers a, la suite des (f(xn))n1 converge vers l.
Preuve :
Supposons que f admet l pour limite lorsque x tend vers a. On veut voir que si (xn)n1 est une suite de points de A
qui converge vers a alors la suite des (f(xn))n1 converge vers l.
  >0,  >0 tel que (x  A et | x – a |<) => |f(x) – l |< )
Soit (xn)n1 convergente vers a. Soit >0, il existe  possédant la propriété ci dessus (la définition de la limite).
On a donc vérifié que   >0,  >0 tel que (x  A et | x – a |<) => |f(x) – l |< . C’est à dire que (f(xn))n1
converge vers l.
On va montrer maintenant que si f ne tend pas vers l lorsque x tend vers a alors il existe une suite (xn)n1 de
points de A telle que (f(xn))n1 ne converge pas vers l. Il s’agit donc de démontrer la négation de la définition de
la limite :   > 0,  >0, il existe x  A tel que | x – a | <  et |f(x) – l |.
Considérons cet  >0 et soit n  N* et =1/n. Il existe xn  A tel que | xn – a | < 1/n et |f(xn) – l| . La suite
(xn)n1 converge vers a et la suite des (f(xn))n1 ne converge pas vers l.
Corollaire :
Soient f, g : AR, a  /A. Supposons que limxa x Af(x) = l et limxa x Ag(x) = l’ alors l et l’ sont uniques. De
plus :
1) limxa x Af(x)+g(x) = l + l’
limxa x Af(x)-g(x) = l – l’
limxa x Af(x)g(x) = l*l’
2) Si l0, il existe >0 tel que 1/l est défini pour x ]a - , a + [A et
limxa xA]a - , a + [ 1/f(x) = 1/l
Preuve :
Utiliser les propriétés correspondantes pour les suites.

2
Critère de Cauchy :
Soient f : A  R, a  /A, alors f admet une limite l lorque x tend vers a si et seulement :
  >0,   >0 tel que (x, x’  A et |x – a | <  et | x’ – a | >  => |f(x) – f(x’) | < .
2 CONTINUITE
2.1 DEFINITION
Soit f : A  R et a  A, on dit que f est continues au point a si et seulement si :
  > 0   > 0 tel que  x  A |x – a |< => |f(x) – f(a) | < . C’est à dire limxa x  A f(x) = f(a).
On peut en déduire la proposition suivante :
f : A  R, a  A, f est continue en a si et seulement si pour toute suite (xn)n1 de points de A qui converge vers
a, la suite des (f(xn))n1 converge vers f(a).
2.2 COROLLAIRE DE LA DEFINITION :
Soient f, g : A  R, a  A. Si f et g sont continues en a alors :
1 – f+g, f-g, f*g sont continues en a
2 – si f(a)0, il existe >0 tel que 1/p est définie sur [a - , a+]  A et 1/p est continue en a.
D’ou, nouvelle proposition :
f : A R, f continue en a et g : B  R avec f(A)  B, g continue en f(a). Alors gof est continue en a.
3 PROPRIETES DES FONCTIONS CONTINUES SUR UN
INTERVALLE
3.1 THEOREME 1
Soit a<b  R, f : [a, b]R continue en tout point de [a, b]. Alors f est bornée sur [a, b] (c’est à dire il existe m,
M  R tels que  x  [a, b], mf(x)M.
Preuve :
On va d’abord démontrer que f est majorée sur [a, b]. On raisonne par l’absurde : supposons que f n’est pas
majorée sur [a, b].
Soit donc n  N*, puisque n n’est pas un majorant de f sur [a, b], il existe xn  [a, b] telle que f(xn)>n. faisant
varier n, on obtient une suite (xn)n1 de points de [a, b]. La suite (xn)n1 est une suite bornée. Par corollaire du
théorème de Bolzano Weierstrass, il existe une suite extraite de (xn)n1 qui est convergente.
On peut donc trouver  : N  N
n  (n) strictement croissante, telle que la suite des (x(n))n1 est convergente.
Soit x0 la limite de la suite (x(n))n1, on a ax(n)b pour tout n  N. D’ou ax0b.
Maintenant, f est continue en x0, donc la suite des (f(x(n)))n1 tend vers f(x0)
  > 0  N  N /  nN | f(x(n) – f(x0) | < . En particulier pour  =1, on trouve N1 tel que si nN1 alors
|f(x(n)) – f(x0) |<1, donc en particulier f(x(n))<f(x0) +1  nN1.
Donc, en particulier, pour nN1 on a (n)<f(x((n))<f(x0) + 1. Or, comme  : NN est strictement croissante, on
a (n)>n. Par suite, on a  n N1, nf(x0)+1. ce qui est absurde, donc f est majorée sur [a, b].
Idem pour minorée.
3.2 THEOREME 2
On considère f([a, b]) = {y  R /  x  [a, b] tel que f(x)=y}  R. Le théorème précédent dit que f est une partie
bornée de R. Par suite, f([a, b]) est une partie non vide majorée (respectivement minorée) de R donc, par
propriété des réels, elle admet une borne supérieure M et une borne inférieure m.

3
On note M= Sup(f([a, b]))= Supx  [a, b] f(x)
m = Inf(f([a, b]))= Infx  [a, b] f(x)
D’ou le théorème suivant :
Soit a<b  R et f : [a, b] R continue sur [a, b].
On pose M = Supx  [a, b] f(x) et m = Infx  [a, b] f(x).
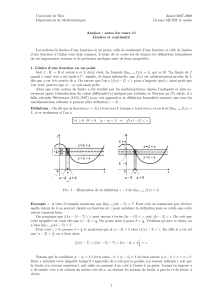
Alors il existe  et   [a, b] tels que f()=m et f()=M. (donc, une fonction continue sur un intervalle fermé
borné admet un maximum et minimum).
3.3 THEOREME 3
Propriété des valeurs intermédiaires :
Soient f : [a, b] R continue sur [a, b]
Soient M = Supx  [a, b] f(x) et m = Infx  [a, b] f(x).
Alors f([a, b]) = [m,M], il existe x  [a, b] tel que y=f(x). En particulier si x1, x2 sont deux éléments de [a, b]
alors toute valeur comprise entre f(x1) et f(x2) est une valeur prise par la fonction.
Corollaire du théorème 3 : théorème des valeurs intermédiaires :
Soient f : IR, une fonction continue sur I, ou I est un intervalle quelconque, alors f(I) est un intervalle, ou
f(I)={y  R / y=f(x)}.

4
A Retenir
Définitions Limite d’une fonction réelle :
Limites vers l’infini : Propriétés des limites :
Critère de Cauchy :
Définitions Continuité :
Propriétés sur la continuité : Propriétés des fonctions continues sur un intervalle
Corollaire du théorème 3 :
théorème des valeurs intermédiaires :
Soit A une partie de R et un point a  R, a est adhérant à A si
et seulement si   > 0, [a-, a+]  A  
L’ensemble des points adhérant à A est appelé l’adhérence de
E et est noté /A.
2 - Soit f : A  R, a  /A, on dit que le nombre l  R
est limite de f lorsque x tend vers a si et seulement si :
  >0,  >0 tel que (x  A et | x – a |<) => |f(x) – l
|< .
Soient A une partie non majorée de R, (respectivement non minorée)
et f : A  R, on dit :
f tend vers +¤¤ lorsque x tend vers +¤¤ par valeurs dans A si et
seulement :  M >0,  k >0 tel que (x>K et x  A => f(x)>M)
respectivement : f tend vers +¤¤ lorsque x tend vers -¤¤ par valeurs
dans A si et seulement si :  M>0,  K’ < 0 tel que (x<K’ et x  A
=> f(x) >M)
1 - Soient f :AR, a  A, l  R alors f admet l
pour limite lorsque x tend vers a si et seulement si
pour toute suite (xn)n1 de points de A qui
converge vers a, la suite des (f(xn))n1 converge
vers l.
2 - Soient f, g : AR, a  /A. Supposons que
limxa x Af(x) = l et limxa x Ag(x) = l’ alors l et
l’ sont uniques. De plus :
1) limxa x Af(x)+g(x) = l + l’
limxa x Af(x)-g(x) = l – l’
limxa x Af(x)g(x) = l*l’
2) Si l0, il existe >0 tel que 1/l est défini
pour x ]a - , a + [A et
limxa xA]a - , a + [ 1/f(x) = 1/l
Soient f : A  R, a  /A, alors f admet une limite l lorque x tend vers
a si et seulement :   >0,   >0 tel que (x, x’  A et |x – a | <  et |
x’ – a | >  => |f(x) – f(x’) | < .
1 - Soit f : A  R et a  A, on dit que f est
continues au point a si et seulement si :
  > 0   > 0 tel que  x  A |x – a |< => |f(x) –
f(a) | < . C’est à dire limxa x  A f(x) = f(a).
2 - Soient f, g : A  R, a  A. Si f et g sont continues en a alors :
1 – f+g, f-g, f*g sont continues en a
2 – si f(a)0, il existe >0 tel que 1/p est définie sur [a - ,
a+]  A et 1/p est continue en a.
1 - f : A  R, a  A, f est continue en a si et seulement si pour toute suite
(xn)n1 de points de A qui converge vers a, la suite des (f(xn))n1 converge
vers f(a).
2 - f : A R, f continue en a et g : B  R avec f(A)  B, g continue en
f(a). Alors gof est continue en a.
1 - Soit a<b  R, f : [a, b]R continue en
tout point de [a, b]. Alors f est bornée sur [a,
b] (c’est à dire il existe m, M  R tels que 
x  [a, b], mf(x)M.
3 – (propriété des valeurs intermédiaires)
Soient f : [a, b] R continue sur [a, b]
Soient M = Supx  [a, b] f(x) et m = Infx  [a, b] f(x).
Alors f([a, b]) = [m,M], il existe x  [a, b] tel que y=f(x). En particulier si
x1, x2 sont deux éléments de [a, b] alors toute valeur comprise entre f(x1)
et f(x2) est une valeur prise par la fonction.
2 - Soit a<b  R et f : [a, b] R continue sur [a, b].
On pose M = Supx  [a, b] f(x) et m = Infx  [a, b] f(x).
Alors il existe  et   [a, b] tels que f()=m et f()=M. (donc, une
fonction continue sur un intervalle fermé borné admet un maximum et
minimum).
Soient f : IR, une fonction continue sur I,
ou I est un intervalle quelconque, alors f(I)
est un intervalle, ou f(I)={y  R / y=f(x)}.