Conductimétrie

Conductimétrie, apports théoriques
Ce document, conçu pour les enseignants, comporte deux grandes parties :
La première partie donne des éléments théoriques sur la conductivité des solutions
d’électrolytes : rappels de vocabulaire et définitions (électrolytes « forts »
1
, électrolytes
« faibles », conductivité, conductance, conductivité molaire, conductivité molaire ionique, etc.)
comportement des ions (mobilité d’un ion placé dans un champ électrique uniforme), relations
entre la conductivité et des grandeurs telles que l’intensité du courant, les concentrations
molaires des ions présents dans la solution.
La deuxième partie traite des titrages conductimétriques. La conductance a été choisie en classe
de première scientifique comme grandeur physique parce que, sous certaines conditions, elle
est reliée de manière linéaire à la concentration molaire ; cette observable permet de suivre une
transformation chimique, et donc de réaliser des titrages acido-basiques. Après avoir montré
l’influence de la dilution au cours d’un titrage conductimétrique (et proposé des remèdes
lorsqu’elle celle-ci n’est pas négligeable), différents titrages sont proposés :
- acide chlorhydrique par une solution de soude,
- solution d’ammoniac par de l’acide chlorhydrique,
- solution d’acide éthanoïque par une solution de soude.
Remarque importante : quel que soit le titrage réalisé, il importe de toujours mettre dans le
becher l’électrolyte «fort» afin de ne pas avoir à justifier la valeur de la conductivité initiale de
la solution ; en effet il y a ionisation plus ou moins partielle de l’électrolyte «faible» dans l’eau
(ces notions sont hors programme en Première S).
A. Quelques généralités
L’eau pure conduit très peu le courant électrique, sa conductivité est due aux ions
oxonium (hydronium) H3O+ et hydroxyde HO- qui viennent de l’autoprotolyse de l’eau :
2 H2O = H3O+ + HO-(aq) Kr = Ke = [H3O+].[HO-]
Ke = 10-14 à 25°C alors [H3O+] = [HO-] = 10-7 mol.L-1, ce qui est très petit.
Soit I0 l’intensité du courant mesurée sous une tension U.
Lorsqu’un composé est dissous dans l’eau (ce composé est le soluté et l’eau le solvant), deux
cas peuvent se produire :
 l’intensité I du courant reste égale à I0 : cas de l’éthanol, du glucose, etc. ; la mise en
solution ne fait pas apparaître d’ions supplémentaires, il y a solvatation des molécules de soluté
par les molécules d’eau par des interactions de Van der Waals ou/et des liaisons hydrogène :
CH3CH2OH(l)  CH3CH2OH(aq)
 l’intensité I du courant devient plus grande que I0 : cas des solutions de chlorure de
sodium, d’hydroxyde de sodium, de chlorure d’hydrogène, d’acide nitrique, de chlorure
d’ammonium, d’acide acétique, d’acétate de sodium, etc. ; des ions supplémentaires sont
apparus, la solution est alors appelée solution électrolytique et le composé qui a apporté les ions
est l’électrolyte.
1
Les appellations, électrolyte fort/faible, acide fort/faible, base forte/faible sont actuellement conservées mais ce
vocabulaire n’est pas introduit auprès des élèves y compris en Terminale S.

Il existe deux catégories d’électrolytes :
 Les électrolytes « forts », qui sont des espèces chimiques qui se dissocient totalement
dans l’eau. Le système chimique ne contient que des ions solvatés dans l’état final :
- NaCl(s)
 Na+(aq)
+ Cl-(aq)
-
NaOH(s)
 Na+(aq)
+ HO-(aq)
- HCl(g)
 H+(aq)
+ Cl-(aq)
- HNO3(l)
 H+(aq)
+ NO3-(aq)
 Les électrolytes « faibles », qui sont des espèces chimiques qui ne se dissocient pas
totalement dans l’eau sous forme d’ions solvatés :
- NH4Cl(s)
 NH4+(aq) + Cl-(aq)
puis
NH4+(aq) + H2O
=
NH3(aq) + H3O+
- CH3COOH(l)
 CH3COOH(aq)
puis
CH3COOH(aq) + H2O
=
CH3COO-(aq) + H3O+
- CH3COONa(s)
 CH3COO-(aq) + Na+(aq)
puis
CH3COO-(aq) + H2O
=
CH3COOH(aq) + HO-(aq)
B. Rappels théoriques sur la conductivité d’une solution électrolytique
1. Conductivité et mobilité
Rappelons pour commencer quelques notions concernant la mobilité des électrons dans un fil
métallique et sa relation avec la conductivité du matériau.
Dans un conducteur métallique, le nombre de charges par unité de volume susceptibles de se
déplacer est une donnée du conducteur (de l’ordre de un électron par atome). Sa résistivité (ou
sa conductivité), fonction de la température, résulte des frottements des charges sur le réseau
des ions immobiles. La vitesse moyenne des électrons (dite aussi vitesse de dérive) est
proportionnelle au champ électrique appliqué (mais en sens opposé) :
E.v 
où désigne la mobilité des électrons. Si l’on désigne par n le nombre d’électrons de
conduction par unité de volume et par e la charge élémentaire, la densité de courant a pour
expression
E..e.nv.e.nj 
Rappelons comment établir cette formule :
I =
dt
dq
dq = - n.e.S.v.dt
I = - n.e.S.v
j = - n.e.v
soit vectoriellement
v.e.nj 
La conductivité du matériau (l’inverse de sa résistivité) est, par définition, égale au coefficient
de proportionnalité entre
j
et
E
. Elle est donc donnée par :
= n.e.
Pour un conducteur de section S, le courant a pour expression I = j.S, et le champ électrique, en
valeur algébrique, est relié à la différence de potentiel aux extrémités A et B du conducteur de
longueur L :
E = (VA – VB)/L. On peut donc écrire :
ℓ
i
e-
ν
S

)VV(
LS.
IBA 
ce qui n’est autre que la loi d’Ohm.
La conductance du fil (l’inverse de sa résistance) est alors égale à
L
S
.G
Dans une solution électrolytique,
- la densité des charges varie en fonction de la concentration,
- les cations, ions positifs, sont mobiles aussi bien que les anions, charges négatives,
- les frottements dépendent de la taille des ions solvatés et de la nature du solvant. Les
mobilités sont donc différentes pour chaque type d’ion.
Pour rendre compte de la conductivité d’une solution électrolytique, il est donc nécessaire
d’expliciter tous ces degrés de liberté.
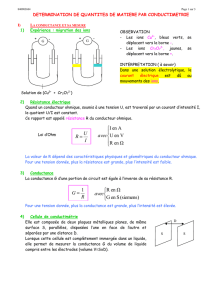
Commençons par un cas simple : celui d’une solution de chlorure de sodium, de concentration
molaire c. On plonge dans cette solution deux plaques métalliques parallèles, de même surface
S, distantes l’une de l’autre d’une longueur L (figure 1). Quand une tension U est appliquée
entre ces deux plaques, il circule un courant d’intensité I dans la solution. Le passage de ce
courant correspond au déplacement des ions présents dans la solution sous l’action du champ
électrique
E
existant entre les deux plaques.
(figure 1)
Sous l’effet de ce champ, chaque type d’ion acquiert une vitesse limite proportionnelle au
champ. Les ions positifs se déplacent dans le sens du champ, les ions négatifs dans le sens
opposé. On a donc :
E.v )()(
l
E.v )()(
l
où
(+) et (-) désignent les mobilités des ions Na+ et Cl- respectivement. Les deux types d’ions
contribuent à la densité de courant totale
j
. Exprimons les charges par unité de volume à l’aide
U> 0
Solution
électrolytique
)(
l
V
E
)(
l
V
A
B

de la concentration molaire de soluté c. En désignant par NA la constante d’Avogadro, e la
charge élémentaire, F = e.NA la constante de Faraday (1 F = 96486 C. mol-1 96500 C. mol-1),
la charge positive par unité de volume est égale à [Na+].e.NA = c.F et la charge négative par
unité de volume est –[Cl-].e.NA = -c.F. Par conséquent la densité de courant totale s’écrit :
La conductivité molaire de la solution, coefficient de proportionnalité entre la densité de
courant et le champ électrique, est donc égale à :
).(F.c.F].Cl[.F].Na[)()()()( 
Dans le cas d’un électrolyte «fort» qui se dissocie suivant l’équation :
)aq(X.b)aq(M.aXM ab
b
a 
En désignant toujours par c la concentration molaire apportée du soluté MaXb, la concentration
molaire en ion Mb+ est égale à a.c, et le nombre de charge positives par unité de volume est
égal à a.b.c.F. La concentration molaire en ion Xa- est égale à b.c, et le nombre de charges
négatives par unité de volume est aussi égal à a.b.c.F (la neutralité électrique doit être
respectée). La conductivité de la solution devient donc :
).(F.c.b.a.F].X.[a.F].M.[b)()()(
a
)(
b
relation (1)
La conductance de la solution est reliée à sa conductivité par une relation de la forme
= G.Kcell
où la constante Kcell dépend de la géométrie de la cellule. Pour une cellule constituée de deux
plaques parallèles de surface S et distantes de L, la géométrie est la même que celle du fil
conducteur, et l’on a Kcell = L/S.
La résistance de la solution emprisonnée entre les deux plaques est :
R = .
S
L
R est la résistance (unité : ohm, )
est la résistivité (unité : ohm.mètre, .m)
La conductance G de la solution est l’inverse de la résistance R , donc
G =
R
1
= .
L
S
Remarque : L’ordre de grandeur de la mobilité d’un ion solvaté peut être obtenu en utilisant un
modèle mécanique dans lequel sa vitesse limite résulte de l’équilibre de deux forces : la force
due au champ électrique et une force de frottement fluide visqueux, représentée par exemple
par la loi de Stokes. Si l’on assimile l’ion solvaté, de charge be, par une sphère de rayon R,
l’équation de la dynamique donne immédiatement, pour la vitesse limite (accélération nulle) :
)(
l
v..R..E.e.b  6
, où désigne la viscosité du liquide. La mobilité qui résulte de ce modèle
est donc donnée par = b.e/6. .R. . Pour un ion monochargé, de rayon R 0,3 nm, dans l’eau
E)..(F.c)vv.(F.cjjj )()()(
l
)(
l
)()( 

(viscosité = 10-3 Pa.s), on trouve 3 10-8 m2.V-1.s-1, ce qui correspond bien à l’ordre de
grandeur des valeurs mesurées. Réciproquement, l’utilisation du modèle, connaissant la
mobilité d’un ion à partir de mesures de conductimétrie, permet d’estimer la taille des ions
solvatés. Il ne faut cependant pas prendre ce modèle trop au sérieux : est-il vraiment justifié
d’utiliser la loi de Stokes à l’échelle atomique, alors qu’il s’agit d’une loi macroscopique
(fluide continu) déduite de l’hydrodynamique, en imposant des conditions particulières au
champ des vitesses du fluide au contact avec le mobile en déplacement ?
2. Conductivité molaire ionique
 Dans la relation (1), le produit b.
(+).F est appelé conductivité molaire du cation
b
M
et est
noté (Mb+). Le terme a.
(-).F est la conductivité molaire de l’anion
a
X
et est noté (Xa-).
Il s’agit de conductivités molaires ioniques.
Dans le cas d’une solution contenant plusieurs ions de conductivité molaire ionique (Xi), de
concentration molaire [Xi], dont le nombre de charges est zi , la conductivité a pour
expression :
=
i
[Xi]. (Xi)
λ(Xi) = zi.F.μi
(relation 2a)
La conductivité s’exprimant en S.m-1 et la concentration molaire [ Xi ] en mol.m-3, la
conductivité ionique molaire s’exprime en S.m2.mol-1.
Exemples
La conductivité d’une solution de chlorure de baryum, BaCl2, de concentration molaire c
s’écrit :
= [ Ba2+ ]. (Ba2+) + [ Cl- ]. (Cl-) = c.[ (Ba2+) + 2. (Cl-)]
La conductivité d’une solution de sulfate de sodium, Na2SO4, de concentration molaire c
s’écrit :
= [ Na+ ]. (Na+) + [
2
4
SO
]. (SO
2
4
) = c.[2. (Na+) +(SO
2
4
)]
 Plutôt que les conductivités molaires ioniques, on trouve dans les tables le produit
i.F de
la mobilité d’un ion par la constante de Faraday. Il s’agit donc de la conductivité molaire
ionique rapportée à une mole de charge. Elle est égale à
.
zi
1
(Xi), zi désignant le nombre
de charges (toujours positif) portées par l’ion Xi, mais on la désigne également par le
symbole
i
Z
(1
Xi).
(
i
z
1
Xi) =
.
zi
1
(Xi) = μi.F
La conductivité de la solution s’écrit alors :
=
ii
i
ii X
z
Xz 1 ..
relation 2b
Exemples : (SO
2
4
) = 2. (1/2 SO
2
4
)