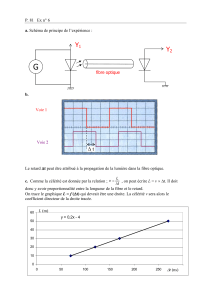
NOM

Physique chapitres 2 et 3
Lumière et mesures de longueurs
1. Sources de lumière.
On ne voit pas la lumière, seulement les objets qui émettent de la lumière : on parle alors de
sources de lumière.
 Source primaire : produit elle-même la lumière qu'elle émet (étoiles, Soleil, lampe...).
 Source secondaire : émet de la lumière parce qu'elle est éclairée, en général par une
source primaire. Elle diffuse la lumière qu’elle reçoit (la Lune, tout objet de cette Terre
lorsqu'il est visible).
Tout objet visible émet de la lumière.
2. Propagation rectiligne de la lumière.
Dans un milieu transparent et homogène, la propagation de la lumière est rectiligne.
2.1. Modèle du rayon lumineux.
Un faisceau lumineux est constitué d’une infinité de rayons lumineux représentés par des
portions de droites orientées dans le sens de propagation.
2.2. Alignement.
La vérification de l’alignement de plusieurs points (par
exemple pour vérifier si la règle est droite) part du
principe que la lumière se propage en ligne droite.
2.3. Dimensions apparentes.
La longueur apparente d’un objet est
l’angle  délimité par les directions de
visée de deux extrémités de cet objet.
Le diamètre apparent d’une sphère est
l’angle  sous lequel elle est vue depuis
un point.
 Deux objets ont même dimension apparente pour un
observateur s’ils sont vus sous des angles égaux.
L’observateur a alors l’impression que ces objets ont
même dimension.
Cette propriété a été utilisée pour déterminer par visée la
hauteur de l’arbre en exercice et celle du grand atelier en
TP.
D
d
H
h
(théorème de Thalès)
faisceau divergent
faisceau convergent
faisceau parallèle
alignement
A
B
C
oeil
oeil
A
B
longueur apparente
oeil
diamètre apparent
h
H
D
d
oeil

Physique chapitres 2 et 3
 Lors d’une éclipse totale de Soleil, la Lune cache presque exactement le Soleil : ces deux
astres ont pratiquement le même diamètre apparent. Cette propriété a été utilisée pour déterminer
le diamètre du Soleil.
Exercice..
Distances de centre à centre : Terre - Soleil : TS = 1,50.108 km
Terre - Lune : TL = 3,84.105 km
Diamètre de la Lune : DL = 3,48.103 km
a. Faire un schéma correspondant à une éclipse totale de Soleil.
b. En déduire une valeur approchée du diamètre du Soleil.
Un astre peut être considéré comme un objet
ponctuel si son diamètre apparent est inférieur
à 3 x 10-4 rad (environ 1/60ème de degré, cette
valeur correspond au pouvoir séparateur de l’œil).
Pour les petits angles ( < 10° soit 0,175 rad), on
montre la relation générale :
tan   sin   rad. sachant que  rad = 180°
De plus, toujours pour les petits angles, on a quelque
soit la nature du triangle :
D
d
αtan 
, soit
D
d
αrad 
Exercice.
La mesure au télescope du diamètre apparent de la Lune a donné le résultat suivant :  = 0,52°.
On adoptera la valeur moyenne 384 000 km pour la distance Terre-Lune.
a. Calculer la valeur de  en radians. Vérifier la relation des petits angles (tan   sin  
rad), à l’aide de la calculatrice.
b. En déduire une valeur approchée du diamètre de la Lune.
c. La Lune peut-elle être considérée par l’observateur comme un objet ponctuel ? justifier.
2.4. La parallaxe.
La parallaxe est la modification apparente de la position d’un objet par rapport à un autre
plus éloigné lorsqu’on change de point d’observation.
 La position d’un objet semble modifiée selon qu’on l’observe de l’œil droit ou de l’œil
gauche..
 La méthode de détermination d’une
distance par triangulation (distance du
bateau, largeur du stade en TP) utilise
la parallaxe.
Cette méthode est utilisée pour
déterminer la distance de la Terre au
Soleil ou de la Terre à des étoiles
proches.
d
D
d
D
A
Ecliptique
B
Terre
E
étoile
proche
Soleil
parallaxe

Physique chapitres 2 et 3
3. La diffraction de la lumière.
Il est impossible d’isoler physiquement un rayon lumineux en raison du phénomène de
diffraction.
Ce phénomène se manifeste lorsque la lumière
rencontre un obstacle de petite dimension (fente
étroite, fil fin, voile à mailles très fines).
L’étude de la figure de diffraction peut permettre de
déterminer des petites dimensions (prochain TP).
4. La vitesse de la lumière.
Dans un milieu transparent homogène, la lumière se propage à vitesse constante. La vitesse de
propagation est encore appelée célérité.
Dans le vide la célérité est c = 2,99792458.108 m.s-1.
Nous retiendrons, dans le vide mais aussi dans l’air, la valeur :
c = 3,00.108 m.s-1, soit 300 000 km.s-1.
Dans les autres milieux transparents la célérité est inférieure à c. La théorie actuelle admet que la
vitesse de la lumière dans le vide est une vitesse limite qu’aucun objet ne peut atteindre ni
dépasser.
Dans le verre, la célérité est voisine de 2.108 m.s-1.
Expression de la distance d parcourue par la lumière en fonction de la célérité c et de la
durée t.
d = c.t. Préciser les unités.
Exercice. Combien de temps la lumière du Soleil met-elle à nous parvenir ? La distance Terre-
Soleil est voisine de 1,50.108 km
4.1. L’année de lumière (a.l.).
L’année de lumière est la distance parcourue par la lumière dans le vide en une année.
Calculer sa valeur, en mètres, à l’aide de la calculatrice utilisée en mode scientifique.
1 a.l. =
Vérifier qu’elle est voisine de 10 000 milliards de kilomètres.
Voyager loin, c’est voyager tôt.
L’étoile Polaire est située à environ 470 années de lumière de la Terre.
Cela fait combien de milliards de kilomètres ?
La lumière que nous recevons actuellement a été émise il y a combien d’années ? Sous le règne
de quel roi.
En analysant la lumière des galaxies les plus éloignées, on obtient ainsi des renseignements sur
la composition de l’Univers à des périodes très éloignées, pratiquement l’origine de l’Univers.
diffraction de la lumière

Physique chapitres 2 et 3
4.2. La technique de l’écho laser.
C’est une méthode de mesure de distances qui
consiste à mesurer la durée qui sépare l’émission
d’un signal lumineux émis par un laser de sa
réception après réflexion sur l’objet étudié.
Elle est adaptée aux très grandes distances (suivi de la trajectoire de la Lune, positionnement
d’un satellite, étude de la Terre vue d’un satellite).
Une technique analogue, dite de l’écho radar, utilise un signal de lumière non visible aux
propriétés analogues (signal radar).
Pour mesurer des petites distances sur Terre, on peut utiliser des signaux ultrasonores qui n’ont
pas les mêmes propriétés que la lumière (vitesse de propagation 340 m.s-1). C’est le principe du
sonar.
Ceci sera étudié au cours d’un prochain TP.
La distance Terre-Lune.
En 1969, les astronautes Armstrong et Aldrin ont déposé sur la Lune un réflecteur de rayons
laser. Une impulsion lumineuse, émise depuis la Terre, effectue l’aller-retour Terre-Lune en une
durée mesurable avec une très grande précision.
1. Au cours d’une mesure, on a trouvé une durée t = 2,704 046 s. Quelle était la distance
Terre-Lune le jour de cette mesure (et d’ailleurs pourquoi cette précision) ? On prendra pour
la vitesse de propagation de la lumière la valeur c = 299 792 458 m.s-1.
2. La durée est mesurée avec une précision de l’ordre du millionième de seconde.
En déduire l’ordre de grandeur de la précision sur la mesure de la distance Terre-Lune.
3. Exprimer la valeur de la distance Terre-Lune avec le nombre de chiffres significatifs
convenable.
émetteur
récepteur