Exploration de l`espace - Exercices

Exploration de
l’espace - Exercices
I. Enoncés
!"
Exercice I
• Partie I
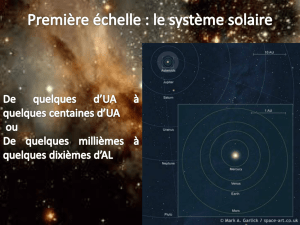
On désire représenter sur une échelle les ordres de grandeurs des
longueurs de l’extrêmement petit à l’extrêmement grand. Pour cela, on
considère les dimensions suivantes :
- Diamètre de l’atome d’hydrogène : 0,1.10
-9
m.
- Longueur d’une bactérie : 9 µm.
- Hauteur d’un homme : 1,90 m.
- Altitude du Mont Blanc : 4807 m.
- Rayon de la Terre : 6,4.10
3
km.
- Distance moyenne Terre-Lune : 3,8.10
5
km.
- Distance moyenne Soleil-Terre : 1,5.10
8
km.
1 – Donner les ordres de grandeur des dimensions données dans
l’énoncé.
2 – Tracer un axe orienté gradué de 25 graduations.
La graduation centrale correspond à 1m.
On passe d’une graduation à la suivante en multipliant la valeur
correspondante par 10.
Placer sur l’axe les différents ordres de grandeurs de la question 1.
3 – Montrer que cette échelle n’est pas linéaire.
4 – Ecrire en toutes lettres (en utilisant les termes ‘milliers’, ‘millions’
ou ‘milliard’) les distances Terre-Lune et Soleil-Terre.
• Partie II
1 – Rappeler la valeur de la vitesse de la lumière avec deux chiffres
significatifs.
2 – Quel est le temps mis par la lumière pour parcourir les distances
séparant la Terre de la Lune et le Soleil de la Terre ?
3 – a – Rappeler la définition d’une année de lumière.
b – Calculer la valeur d’une année de lumière en kilomètres.
c – Convertir la distance Soleil-Terre en année de lumière.
Commenter le résultat.
!"
Exercice II
Un observateur place une pièce de 2 euros à 2,7 m de son œil de
façon à occulter exactement la Lune dans le ciel. La pièce de 2 euros
à un diamètre de 2,5 cm, et l’observateur a trouvé dans un dictionnaire
une distance moyenne Terre-Lune de 3,8.105 km.
Quel le diamètre approximatif de la Lune ?
II. Corrigés
!"
Exercice I
• Partie I
1 -
- Diamètre de l’atome d’hydrogène ≈ 10-10 m.
- Longueur d’une bactérie ≈ 10-5 m .
- Hauteur d’un homme ≈ 1 m.
- Altitude du Mont Blanc : entre 103 et 104 m.
- Rayon de la Terre : 6,4.103 km = 6,4.106 m ≈ 107 m.
- Distance Terre-Lune : 3,8.105 km = 3,8.108 m ≈ 108 m.
- Distance Soleil-Terre : 1,5.108 km = 1,5.1011 m ≈ 1011 m.
2 -
3 – Entre la graduation 1 et la graduation 10, il y a une longueur de 9
m. Dans un même intervalle, entre les graduations 102 et 103, il y a
900 m. La longueur n’est pas la même entre deux graduations
successives. Donc cette échelle n’est pas linéaire.
4 – 3,8.105 km = 380.103 km et 103 représente un millier.
La distance Terre-Lune est donc 380 milliers de kilomètres.
1,5.108 km = 150.106 km et 106 représente un million.
La distance Soleil-Terre est donc 150 millions de kilomètres.
• Partie II
1 – La vitesse de la lumière dans le vide vaut 3,0.105 km/s.
2 – v = d
t donc t = d
v .
Pour la distance Terre-Lune :
t = d
v = 3,8.105 km
3,0.105 km/s ≈ 1,3 s.
Pour la distance Soleil-Terre :
t = d
v = 1,5.108 km
3,0.105 km/s ≈ 500 s = 8 min 20 s.
3 – a – Une année de lumière (a.l.) est la distance parcourue par la
lumière, dans le vide, pendant une année.
b – 1a.l. = v.t
avec v = 3,0.105 km/s
et t = 1 année = 365 j = 8760 h = 31536000 s.
1 a.l. = 3,0.105 x 31536000 = 9,46.1012 km.
c - 1,5.108 km = 1,5.108
9,46.1012 a.l. = 1,6.10-6 a.l.
L’année lumière est une très grande unité. Elle n’est pas vraiment
adaptée aux dimensions du système solaire mais plutôt aux
distances séparant les étoiles ou les galaxies dans l’Univers.
!"
Exercice II
Le diamètre apparent de la Lune est le même que celui de la pièce de
2 euros.
D’après le schéma ( en utilisant le théorème de Thalès) :
OM
ON = d
D donc D = d.ON OM = 2,5.10-2 x 3,8.108
2,7 ≈ 3,5.106 m.
MemoPage.com SA © / 2006 / Auteur : Emmanuel Parras