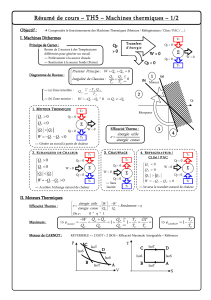
Cycle de Joule

www.kholaweb.com
T5.9. Cycle de Joule
Enoncé.
Une masse m = 1 kg d’air décrit le cycle thermodynamique suivant :
état A : To = 300K, Po =
5
1,0.10 Pa
;
état B :
1
T
,
1o
P kP
état C :
21
1000K, TP
état D :
3,o
TP
transformations AB et CD : adiabatiques réversibles ;
transformations BC et DA : isobares.
L’air est assimilé à un gaz parfait, de capacité calorifique à pression constante
P
C
et de rapport
1,40
.
Constante des gaz parfaits : R = 8,31 S.I
1. Calculer les valeurs des températures
13
et TT
pour k = 10.
Donner l’allure du cycle en diagramme de Clapeyron (P en fonction de V).
2. Faire le bilan énergétique du cycle :
¤ quantités d’énergie thermique échangées ;
¤ travail total : est-il reçu ou fourni ?
De quel type de machine s’agit-il ?
Définir et calculer son rendement (ou efficacité).
3. Les échanges thermiques du fluide ont lieu uniquement avec deux sources :
¤ une source chaude à
2
T
;
¤ une source froide à
o
T
.
Le cycle étudié est-il réversible ? Expliquer pourquoi il l’est ou ne l’est pas.
Que peut-on calculer pour le vérifier numériquement ?
4. Calculer les variations d’entropie de l’air pour les différentes transformations.
Quelles relations doivent vérifier ces différentes quantités ?
5. Le cycle étant décrit dans le sens correspondant à un moteur, et les températures des sources
restant inchangées, exprimer le travail total récupéré en fonction de
2
, , , et
Po
C T T k
.
Quelle valeur doit-on donner à k pour obtenir le travail maximal ?

www.kholaweb.com
T5.9. Cycle de Joule.
Corrigé.
1. Températures.
Une transformation adiabatique, réversible d’un gaz parfait de coefficient γ constant vérifie la loi de
Laplace :
1
p T cte
On peut donc écrire pour les transformations AB et CD :
111
11
1 1 1 1
1
1
579 K
o
o o o o o
p
p T p T T T T T k
pk
T
De même :
11
11 1
1 2 3 3 2 2
3
518 K
oo
p
p T p T T T T k
p
T
2. Bilan énergétique.
Pour les transformations adiabatiques AB et CD on a :
0
AB CD
QQ
Sur une transformation isobare on a
P
Q H C T   
d’où :
1
2 1 2
1
0 3 2
0
1
0
1
BC P o BC
DA P o DA
mR
Q C T T T T k Q
M
mR
Q C T T T T k Q
M
Le gaz décrivant un cycle, on a alors :
1 3 2
0
BC DA P o
U W Q
W Q Q Q C T T T T

11 5
2
1 1 2,0.10 J
1o
mR
W T k T k W
M
Le cycle est parcouru dans le sens horaire. L’aire de ce cycle est positive et correspond donc à
W
car
ext
cycle
W p dV 
. Le travail total est donc négatif et fourni à l’extérieur. Le cycle étudié est moteur
dont le rendement est défini par :
1
121
32
11
21 22
11
2
1
2
1
1 1 1 1
1
1 0,48
BC
o
BC DA o o
DA
BC BC oo
o
o
grandeur utile W
grandeur couteuse Q
T
kT
Q Q T T T k T
Qk
Q Q T T T T k T T k
k T T k
T T k
k
3. Cycle réversible ?
Le cycle étudié n’est pas réversible car les échanges d’énergie par chaleur lors du contact avec les sources
ne se font pas en suivant une transformation isotherme
gaz extérieur
TT
aux différents stades des évolutions
BC et DA.
Pour montrer cela il faut opérer un bilan entropique et montrer que la création d’entropie sur le cycle est
positive.
Le second principe postule que sur un cycle :
22
33
11
22
1
0
22
1
307 J.kg
ec
BC BC
DA DA
ce oo
cP oo
c
S S S
QQ
QQ
SS T T T T
TT
TT
mR
SC
T T M T T
S
4. Variations d’entropie de l’air sur les différentes transformations.
Sur les adiabatiques réversibles (isentropiques) la variation d’entropie est nulle.
Pour les transformations isobares, on utilise l’identité thermodynamique :
pour une transformation isobare
VP
dU p
dS dV
TT nR
pV nRT dV dT
p
dT dT dT
dS C nR C
T T T
On obtient ainsi :
2
13
ln , ln o
BC P DA P T
T
S C S C
TT

Sur le cycle on a :
22
1 3 1 3
2
13
ln ln ln 0
1
oo
P P P
o
TT
TT
S C C C
T T T T
T
T
TT
5. Travail maximal.
D’après la question 2 :
1 3 2
11
2
11
Po
Po
W C T T T T
W C T k T k
Le maximum sera obtenu pour
0
dW
dk 
.
1 1 2 1 1 2
22
1 1 2 1 1 2
22
21
2
1 1 1 0
P o o
oo
o
dW C T k T k T k T k
dk
T k T k T k T k
T
kT