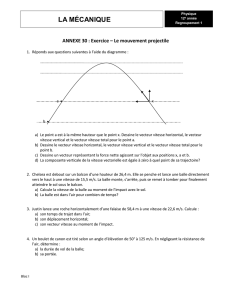
Mouvement d`un projectile dans le champ de pesanteur

Mouvement d’une balle de tennis dans le champ de pesanteur
I -Objectifs :
Rechercher un modèle mathématique du mouvement d’une balle de tennis (voir photo ci-
dessous).
Hypothèse :peut-on considérer que la seule force responsable de celui-ci est le poids de l’objet
ce qui revient a assimiler le mouvement à une « chute libre » (ici avec vitesse initiale de
direction non verticale). Quel serait l’écart entre ce modèle et les résultats expérimentaux.
Quelles sont les autres forces pouvant intervenir ? Peut-on toujours les négliger devant le
poids?
II-Connaissances requises :
Cinématique :
-Mouvements rectiligne uniforme et uniformément varié.
-Construction des vecteurs vitesse et accélération en un point de la trajectoire.
Dynamique :
-Les lois de Newton et leur exploitation dans le but d’établir les équations paramétriques du
mouvement.
III- Détermination du vecteur accélération en un point :
1-méthode graphique de détermination :
-Le document ci-dessous donne les positions successives du mouvement du centre d’inertie
d’une balle de tennis. Le tracé est obtenu à partir du clip vidéo : « parabole tennis ».
-Faire une copie d’écran agrandie de ce document et l’imprimer pour pouvoir travailler
dessus : l’intervalle de temps entre 2 positions successives est : t =0.05s
-Déterminer l’échelle des distances du document sachant que la distance réelle entre 2 traits
de graduation est de 0,305m,
-Choisir un point pour le tracé ; L’auteur a choisi le point d’altitude maximum (point 5 dans les
constructions). Il est intéressant que les groupes d’élèves ne choisissent pas tous les mêmes points,
cela permettra de voir l’évolution éventuelle de l’accélération au cours du mouvement.
Question : après obtention de plusieurs tracés, proposer une expression du
vecteur accélération. Que peut-on dire de ce vecteur au cours du mouvement ?

- Pour revoir les méthodes de tracé de ce vecteur :
point méthode :tracé du vecteur accélération
Correction
-
Tracé obtenu après agrandissement
Evaluons les valeurs des vitesses aux 2 points qui encadrent le point 5.
V4=A3A5/ 2.t= 2,32m.s-1.
V6=A5A7/2.t= 2.31m.s-1.
Construire les vecteurs V6 et –V4 en choisissant le point A5 comme origine commune et en
respectant l’échelle des vitesses: 1cm <->1m.s-1.
Tracer le vecteur variation de vitesse entre A4 et A6, soit
v
.

La longueur de ce vecteur est de 1cm soit :
1
.0,1   smvv
Et comme :
t
vv
t
v
a
.22 46
5
La valeur approchée de l’accélération est :
2
5.10
05.0.2 0,1 
 sma
Et la construction semble monter que sa direction est verticale.
D’autres mesures montreront que le vecteur accélération a même valeur et même direction en
tous les points (aux incertitudes de mesures prés).
Il semble possible d’en déduire que :
ga  
Ce qui rend l’hypothèse d’une chute « libre »vraissemblable
b-étude du mouvement de la balle avec le logiciel Avistep.
Cliquer sur le lien suivant Dossier vidéo
Dans le dossier vidéo, lire le clip vidéo : « parabole tennis » avec Avistep
(L’échelle du document est donnée par l’image ci-dessus)
Tracés à déterminer :
Pointer les positions successives de la balle et demander le vecteur accélération de chaque
point.
On demandera également les tracés en fonction du temps des grandeurs suivantes :
-Projection horizontale de la vitesse vx(t).
-Projection verticale de la vitesse vy(t)
Question :
Les documents obtenus permettent-ils de conclure sur la validité du modèle de la chute
libre ? Justifier la réponse.
Correction

Le graphique ci-dessous confirme que le vecteur accélération est constant et que sa valeur est
proche de 9,8m.s-2.Le modèle de la chute libre semble très satisfaisant
.
Les projections des vitesses :

Vx
Vy
Résultats :
Vx est constant au cours du mouvement.
Vy est une fonction affine décroissante de t.
Conclusion :
Le mouvement de la balle résulte de la composition d’un mouvement rectiligne uniforme
horizontal et d’un mouvement rectiligne vertical uniformément varié.
Ceci est en accord avec les deux lois de Newton de la dynamique et confirme un peu plus
l’hypothèse d’une « chute libre ».
-selon une direction horizontale la balle n’est soumise à aucune force (si l’on néglige les
frottements !) et la 1ére loi (ou principe d’inertie) s’applique, le mouvement projeté sur Ox
est rectiligne et uniforme.
-selon une direction verticale, la balle est soumise à une force constante : le poids et la 2éme
loi s’applique, le mouvement projeté sur Oy est rectiligne et uniformément varié (accéléré
dans la phase descendante et décéléré dans la phase montante).
II Etude théorique du modèle de la chute libre :
a-équations paramétriques du mouvement :
Le système étudié est la balle, de centre d’inertie G.
Nous supposerons que la seule force appliquée est le poids P.
Le référentiel d’étude est la Terre, considéré galiléen. Nous pouvons appliquer la 2ème loi de
Newton.