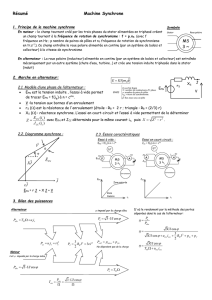
II) Modèle équivalent de la machine

Résumé Machines Synchrones
I) Introduction
Convertisseurs d’énergie mécanique en énergie électrique
(alternateur) ou inversement ( moteur synchrone)
La vitesse de rotation est constante. f = p n .
f : fréquence du réseau et p : nombre de paires de pôles.
MS
~
MS
3~
Induit
Inducteur
Machine
monophasée
Machine
Triphasée
MS
~
MS
3~
~
~
~
1
2
3
~
1
2
3
I.1) Fem induite :
La fem induite par un champ tournant à la vitesse S a
une pulsation  = pS et est égale à :
ˆ
2,22
bf
E K K Nf
K
ˆˆ
S
E KNf KNpn
E : f.é.m. induit (V)
K : coefficient de Kapp
N : nombre de conducteurs d’une phase de la machine
(1 spire = 2 conducteurs)
ˆ
: flux maximum à travers un enroulement (Wb)
f : fréquence du courant statorique
p : nombre de paires de pôles
nS : vitesse de rotation (tr.s-1)
II) Modèle équivalent de la machine :
II.1) Modèle équivalent de Behn Eschenburg pour un enroulement d’alternateur:
EPN
r
X
J
V
iexc
uexc
PN
E
V
J
Jr
JX
/2
PN
PN
E rJ XJ V
E rJ jXJ V
- V (V)est la tension aux bornes d’un enroulement de la
machine
– EPN (V)est la fém à vide ou fém synchrone : elle ne
dépend que de ieN si n est fixée.
– r () est la résistance de l'enroulement : très souvent
négligée.
- X () traduit la chute de tension due à la réaction
magnétique d'induit: elle est appelée réactance
synchrone.
Remarque : le déphasage entre ePN et v est appelé angle
décalage interne. On le note .
II.2) Détermination des éléments du modèle :
II.2.1) Etude à vide et en court circuit détermination de X:
A vide : Le rotor et son champ sont entraînés par une turbine. Les
bobines de l’induit sont alors le siège de f.é.m. alternative de pulsation
 = p.S. alors EPN = K p n N max =K'
La caractéristique EPN = f(ie) est donc identique à celle de la courbe de
magnétisation du circuit.
En court circuit : La caractéristique Jcc = f(ie) à n = cste est une droite
passant par l'origine ( il suffit donc d'une mesure pour la déterminer ).
A l’aide des deux essais on détermine Z.
()
()
PN e
CC e
Ei
ZJi
(pour une valeur de iexc fixée
ATTENTION : EPN et Jcc doivent être obtenus pour une même valeur
de courant d'excitation ie .
JCC
EPN
iexc
EPN
JCC
A
C
B
Caractéristique à vide
Caractéristique en court circuit

II.2.2) Détermination de r
Elle se fait par la mesure de la résistance RB entre phases, par une méthode voltampèremétrique.
r
r
r
Couplage étoile
RB = 2r
Couplage triangle
r
r
r
RB = (2/3) r
II.2.3) Bilan de puissance:
abs M e e
P T u i  
2
je e e e
P u i ri
22
33
2
JB
P R I rJ
coll méca fer
P p p
3 cos
u
P UI
Alternateur
Moteur
3 cos
abs
P UI
uM
PT
imposé par la charge élec
3 cos
em
em PUI
T
Ne dépendent pas de la charge
et imposés par la charge méca
2
3 cos
3
3 cos 2
3 cos
u
abs
exc exc B m f
M exc exc
P
P
UI
UI u i R I p p
UI
T u i
III) Fonctionnement en alternateur.
Couplage des machines synchrones sur le réseau :
Le couplage s’effectue à vide.
- Egalité des tensions efficaces de l’alternateur et du réseau (réglage du courant d’excitation.)
- Egalité des fréquences et des phases (entraînement à la vitesse de synchronisme par le moteur.)
- Même ordre des phases : visualisé à l’aide d’un synchronoscope ou de lampes de couplage.
EPN
X
J
V
iexc
uexc
PN
E
V
J
JX
/2
PN
PN
E XJ V
E jXJ V
cos sin
sin cos
cos cos
XJ E
XJ E V
VE

IV) Fonctionnement en moteur synchrone :
IV.1) Schéma équivalent
EPN
X=L
J
V
PN
V jXJ E PN
E
V
J
JX
cos sin
sin cos
cos cos
XJ E
XJ E V
VE
PN
E
V
J
JX
IV.2) Expression du couple
La puissance électromagnétique est
3 sin
3 cos 3 cos
eV
VE
P VJ E J X
d’où
3 cos
V
eEJ
C
Comme
cos cos
V
EV
alors
3 cos
eVJ
C
Et comme
cos sinXJ E
alors
3 sin
V
eVE
CL
Les trois expressions sont équivalentes
IV.3) Fonctionnement à excitation constante :
PN
E
V
J
JX
P
Pmax
O
A
B
H
Equi puissance
active
Q
Equi puissance
réactive
On considère une machine non saturée. E=cte
OB décrit une circonférence de centre O et de rayon E.
 AB est proportionnel au courant I :
AB X J
 AH est proportionnel à Icos soit P
cos 3
X
AH X J P
V
 BH est proportionnel à Isin soit Q
sin 3
X
BH X J Q
V
Si V, f et ie (donc E) sont constants, Pmax correspond à =/2.
Si le couple résistant est supérieur à Tmax= Pmax/S , le
moteur décroche. (S=2nS=2.f/p).
Pour P donné, AH est constant. Le point de fonctionnement B
se déplace sur une droite parallèle à V dite droite d’équi-
puissance.
Cem
em
T
ˆ
/2
D’après cette expression du couple
3 sin
V
eVE
CL
Il apparaît que le maximum de puissance est atteint pour
=/2

V) BILAN.
PN
E
V
J
XJ
()
exc
i
()J
R
PN
E
V
J
()J
XJ
()
exc
i
()J
R
P
Q
Convention générateur
P>0 : alternateur
P<0 : moteur
Q<0 : bobine
Sous excité
Q>0 : condensateur
Sur excité
-/2 <  <0
PN
E
V
J
XJ
()
exc
i
()J
R
0 <  < /2
PN
E
V
XJ
()
exc
i
()J
R
J
/2 <  < 
PN
E
V
J
XJ
()
exc
i
()J
R
PN
E
V
J
XJ
()
exc
i
()J
R
- <  <-/2
PN
E
V
J
XJ
()
exc
i
()J
R
EP
N
X
J
V
XJ
PN
E
V
J
()J
XJ
()
exc
i
()J
R
-/2 <  <0
0 <  < +/2