6ème -juin-14 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices

6ème -avr.-17 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices - 1 / 19
Chapitre n°20 : Symétrie axiale – Médiatrices, bissectrices
Liste des objectifs :
a. 5ème : [Abordable en 6ème] savoir quelle droite particulière est l’axe de symétrie d’un segment et
savoir la construire.
b. 5ème : [Abordable en 6ème] connaître et utiliser la caractérisation de la médiatrice par
l’équidistance des points.
c. 5ème : [Abordable en 6ème] savoir quelle droite particulière est l’axe de symétrie d’un angle et
savoir la construire.
d. 5ème : [Abordable en 6ème] savoir construire ou compléter une figure symétrique d’une figure
donnée ou de figures possédant un axe de symétrie à l’aide du rapporteur.
Exercice n°1 – EXERCICE DIAGNOSTIQUE – à montrer au professeur
Cet exercice est UN EXERCICE DIAGNOSTIQUE :
- Il faut essayer de le faire UNE SEULE FOIS.
- Il faut ensuite essayer de compléter le cours qui suit.
- Si tu as UNE erreur ou plus, ou si tu NE SAIS PAS REPONDRE, passe
A L’EXERCICE QUI SUIT.
- Si tu as TOUT JUSTE (vérifie-le en regardant les solutions à la fin du
document) et si le COURS EST JUSTE aussi (fais le vérifier par le
professeur), va DIRECTEMENT à l’exercice n°7
- ATTENTION : tu peux quand même avoir une interrogation sur le
cours.
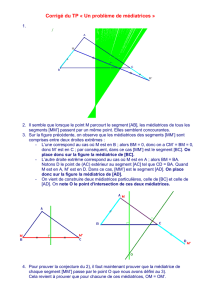
1. Construire à l’aide du compas les médiatrices des segments suivants :
2. Compléter : « Si un point est sur la médiatrice d’un segment, il est à é……………………..
d……………………………. des extrémités du segment. »
3. Compléter : « Si un point est à é…………………….. d…………………………………….. des extrémités
du segment, alors il est sur la médiatrice de ce segment ».
M
N
L
K
SUITE PAGE SUIVANTE

6ème -avr.-17 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices - 2 / 19
Exercice n°2 – INTRODUCTION AU COURS N°1 – INDISPENSABLE POUR
COMPLETER LE COURS - (à montrer obligatoirement au professeur)
ABC est un triangle isocèle en A. On a AB=9,2 cm BC=5,7 cm.
1. Le construire ci-dessous (en utilisant un compas) :
2. On veut construire précisément son ou ses axes de symétrie.
a. Combien en a-t-il ?......
b. Comment doit être l’axe de symétrie du côté [BC] par rapport à
[BC] (deux conditions) ? Condition n°1 :
……………………………………………………………………………………………….
Condition n°2 :
……………………………………………………………………………………………….
c. A l’aide de l’équerre uniquement, construire l’axe de
symétrie de ce triangle.

6ème -avr.-17 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices - 3 / 19
Exercice n°3 – INTRODUCTION AU COURS N°1 – INDISPENSABLE POUR
COMPLETER LE COURS - (à montrer obligatoirement au professeur)
Définition à connaître :
La médiatrice d’un segment est l’axe de symétrie de ce segment.
En utilisant les deux conditions découvertes à l’exercice précédent,
construire les médiatrices (c'est-à-dire les axes de symétrie) des
segments ci-dessous à l’aide de l’équerre et de la règle graduée ou du
compas :
C
B
E
D
G
H
G
H

6ème -avr.-17 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices - 4 / 19
Cours n°1---------------------------------------------
Cours à compléter, à montrer au professeur :
Chapitre n°20 : Symétrie axiale – Médiatrices et bissectrices
I) Médiatrice d’un segment
Définition n°1 :
La médiatrice d’un segment est l’……………………………………………………………… de ce
segment
Propriété n°1
La médiatrice d’un segment passe par …………………………………………… de ce
segment et est …………………………… à ce segment.
Fin du Cours n°1---------------------------------------
Apprentissage du cours
Copier les savoirs, de mémoire, 6 fois, sur une feuille de brouillon, en « accordéon ».
Coller l’accordéon, plié, dans votre cahier de cours (attention : le professeur peut vous
demander de montrer ce travail)
Recopier le cours dans le cahier de cours (à la maison ! ) – Pensez à changer
de page (Nouveau chapitre)
Exercice n°4 – INTRODUCTION DU COURS N°2 – INDISPENSABLE POUR
COMPLETER LE COURS
1. Complétez la figure ci-dessous à l’aide du compas et de la règle sans
se servir des graduations : vous devez construire au moins cinq
triangles isocèles dont la base est toujours [MN].
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
M
N
SUITE PAGE SUIVANTE

6ème -avr.-17 – Chap.n°20–Sym.ax.,p.II:Médiatrices,bissectrices - 5 / 19
2. Que remarquez-vous ?
« les points sont a……………………………et la droite formée par ces points
- est p ……………………………………… à …………………………….
- passe par le m…………………………… de ………………………………..
3. En déduire ce qu’est la droite qui passe par tous ces sommets
principaux.
…………………………………………………………………………………………………………………………………
…………………………………………….
4. Que peut-on dire de la distance des points construits par rapport aux
extrémités du segment MN ?
………………………………………………………………………………………………….
…………………………………………………………………………
5. Complétez : « Si un point est à é………………………… d……………..………………… des
extrémités d’un segment, alors il est sur la ………………………………… de ce
segment.
6. Placez maintenant un point sur cette droite, et mesurez les distances
qui séparent ce point de M et N. Que semble-t-il se passer?
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………….
7. Complétez : « Si un point est sur la ……………………………………………………. De
ce segment, alors il est à ………………………………… ……………………………………… des
extrémités de ce segment. »