exemples de resolution numerique d`equations differentielles

EXEMPLES DE RESOLUTION NUMERIQUE D’EQUATIONS DIFFERENTIELLES
Au cours de la modélisation de la trajectoire d'un obus, nous avons été en présence
d'équations différentielles. Nous avons donc réalisé cette page annexe qui présente les
principales méthodes de résolution possibles de telles équations. Nous allons ici étudier
successivement :
- la méthode d'Euler
- la méthode d'Euler améliorée
- la méthode de Runge Kutta d'ordre 4
1 - La méthode d'Euler
La méthode d'Euler est la plus simple des méthodes de résolution d'équations
différentielles. Sa simplicité est malheureusement proportionnelle à son
imprécision. Cependant, les méthodes plus avancées de résolutions d'équations
différentielles s'appuient généralement sur la méthode d'Euler, aussi allons nous
décrire-celle-ci.
Principe de la méthode :
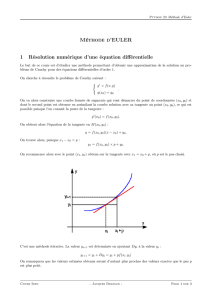
Soit une fonction y(x) et y'(x)=f(x;y) sa dérivée; avec (x0; y0) un point du domaine de l'équation.
La méthode d'Euler consiste à approcher la fonction y(x) par une fonction définie par
segments.
Application :
On étudie f sur un intervalle I=[a; b] avec a et b des nombres réels tels que :
a=x
b=x+n*h ; avec n un entier naturel, et h le pas de temps de l'étude.
On subdivise I en n intervalles : [x0; x0+h]; [x0+h; x0+2h]; [x0+2h; x0+3h]; ... ; [x0+(n-1)h;
x0+nh]
On prend k un entier naturel quelconque compris entre 0 et n. On note :
xk=x0+kh
yk=y(xk)
Ak le point de coordonnées (xk;yk) dans un repère orthonormé
C la courbe représentative de y dans le même repère
Tk la tangente à C en Ak
On veut déterminer les valeurs de xk et yk pour n'importe quel k. Par définition, la tangente à
C en A0 a pour équation:
T0 : y=y(x0)+(x-x0)y'(x0)=y0+(x-x0)f'(x0;y0)
pour x=x1, on a alors: y1=y0+(x1-x0)f(x0;y0)
y1=y0+(x0+h-x0)f(x0;y0)
y1=y0+h.f(x0;y0)
Par un raisonnement analogue, on obtient :
T1 : y=y(x1)+(x-x1)y'(x1)=y1+(x-x1)f'(x1;y1)
et : y2=y1+h.f(x1;y1)
On généralise la relation à tous les k :
xk=x0+kh

yk=yk-1+h.f(xk-1;yk-1)
Etant donné qu'on connaît y0, on peut déterminer par récurrence la valeur de chaque yk
On peut ainsi déterminer les coordonnées de chaque points Ak.
Exemple :
Pour accompagner notre propos, nous avons réalisé un programme (dont vous pouvez voir la
source ici) qui résout l'équation différentielle y'=y et y(0)=1 (dont la solution est
l'exponentielle) sur les valeurs y(1), y(2) et y(3) pour des pas de temps décroissants.
Les résultats vous sont présentés sous la forme d'un tableau ci-dessous.
pas de temps :
1
0.5
0.25
0.125
valeur analytique :
exp(1)
2
2.25
2.44140625
2.56578451395
2.718281828
exp(2)
4
5.0625
5.96046447754
6.58325017203
7.389056099
exp(2)
8
11.390625
14.5519152284
16.8912013428
20.08553692
Courbes représentatives de l'exponentielle :
On note que plus le pas de temps est faible, plus la courbe "numérique" est proche de la
courbe analytique. La précision des résultats dépend donc, en grande partie, de la valeur du
pas de temps choisi.
Vous pouvez voir la source du programme ici

Nous vous présentons les captures d'écran du programme ici
Enfin, nous avons réalisé un autre programme qui vous permet d'obtenir les solutions d'une
équation différentielle selon différents paramètres. Vous pouvez l'utiliser ici.
Conclusion
* Plus le pas de temps est faible, plus le calcul est précis et plus les calculs sont longs. Il faut
donc déterminer un pas de temps qui allie rapidité et précision, ce que nous allons faire dans
la partie modélisation.
* la méthode d'Euler est relativement simple, mais souffre d'une certaine imprécision. Pour y
remédier, nous allons travailler sur une amélioration de cette méthode et sur la méthode de
Runge-Kutta d'ordre 4.
2 - La méthode d'Euler améliorée
la méthode d'Euler améliorée est une méthode qui allie la rapidité et une relative simplicité.
Nous allons donc l'utiliser au cours de la partie modélisation.
Principe de la méthode :
On étudie le développement en série de Taylor au voisinage de x0 de la fonction y(x).
Il nous est donné par la formule y(x0+h)=y(x0)+h.y'(x0)+1/2.h2.y''(x0)+... . On note ainsi que la
méthode d'Euler donne elle une approximation de y(x0+h) : y(x0+h)=y(x0)+h.y'(x0) ; et
tronque donc le développement en série de Taylor au deuxième terme.
De cette troncature, il résulte une erreur d'arrondi de l'ordre de h. Le principe de l'amélioration
de la méthode d'Euler consiste a obtenir une erreur d'arrondi plus faible, de l'ordre de h2.
Application :
On admet, comme pour la méthode d'Euler simple, qu'il existe une fonction F telle que :
yk+1=yk+h.F(xk,yk)
On veut déterminer la fonction F.
On prend k un entier naturel quelconque compris entre 0 et n. On note :

xk=x0+kh
yk=y(xk)
Ak le point de coordonnées (xk;yk)
dans un repère orthonormé
C la courbe représentative de y dans
le même repère
Tk la tangente à C en Ak
Ek le point d'abscissexk, obtenu par
la méthode d'Euler.
Connaissant yk, on calcule yk+1 comme étant l'ordonnée du point d'intersection de la droite (Ek
Ek+2) et de la droite d'équation x=xk+1
La fonction F a pour valeur en xk : F(xk)=a ; avec (Ak Ak+1):y=ax+b , a est la pente de cette
droite.
Ak et Ak+2appartienent à (Ak Ak+2), on a donc :
yk+2=a.xk+2+b (1)
yk=a.xk+b (2)
On soustrait (2) de (1) : yk+2-yk=a.xk+2-a.xk
yk+2-yk=a(xk+2-xk)
yk+2-yk=a(xk+2h-xk)
yk+2-yk=a.2h
soit : a=1/(2h)*(yk+2-yk)
On calcule yk+2 avec la méthode d'Euler :
yk+2=yk+1+h.f(xk+1;yk+1)
yk+2=yk+hf(xk;yk)+h.f[xk+h;yk+hf(xk;yk)]
On introduit la formule de yk+2 dans a :
a=1/(2h)*( yk+2=yk+hf(xk;yk)+h.f[xk+h;yk+hf(xk;yk)]-yk )
a=1/(2h)*h[f(xk;yk)+f[xk+h;yk+hf(xk;yk)]
a=1/2.f(xk;yk)+1/2.f[xk+h;yk+hf(xk;yk)]
soit F(xk;yk)=1/2.f(xk;yk)+1/2.f[xk+h;yk+hf(xk;yk)]
On en déduit la relation par récurrence :
xk=x0+k.h
yk+1=yk+1/2.f(xk;yk)+1/2.f[xk+h;yk+hf(xk;yk)]
Conclusion
Cette amélioration de la méthode d'Euler permet d'obtenir dans des délais relativement courts
; nous l'utiliserons donc dans certains programmes de modélisations.
Cependant, pour des programmes nécessitant d'importantes ressources, nous lui préfèrerons la
méthode de Runge-Kutta.

3 - La méthode de Runge-Kutta d’ordre 4
Runge
La méthode de Runge-Kutta d’ordre 4 est la méthode de
résolution numérique d'une équation différentielle la plus
couramment utilisée. Son efficacité compense sa relative
complexité.
Kutta
Principe de la méthode :
Le principe de la méthode de Runge-Kutta ordre 4 est sensiblement le même que celui de la
méthode d'Euler améliorée.
En revanche, l'ordre de la méthode de Runge-Kutta d'ordre 4 est supérieur à celui de la
méthode d'Euler améliorée, ce qui laisse entrevoir des temps de calcul plus faibles.
Application :
Comme pour la méthode d'Euler améliorée, on approche la pente de la tangente à la courbe;
c'est à dire, qu'on cherche une fonction F telle que :
yk+1=yk+h.F(xk;yk)
On introduit alors trois points auxiliaires, Bn, Cn et Dn
Les points Bn, Cn et Dn sont définis par :
yn0=yn
Bn : yn1=yn+1/2.h.f(xn+1/2.h; yn0)
Cn : yn2=yn+1/2.h.f(xn+1/2.h; yn1)
Dn : yn3=yn+1/2.h.f(xn+1/2.h; yn2)
On approche alors la valeur de la pente f(xn,yn) par la moyenne coefficientée de cette pente
avec les trois valeurs corrigées yn1, yn2 et yn3
yn+1=yn+1/6.h.f(xn+h,yn)+1/3.h.f(xn+1/2.h,yn1)+1/3.h.f(xn+1/2.h,yn2)+1/6.h.f(xn+h,yn3)
Que l'on peut écrire plus simplement :
yn+1=yn+h/6 * (yn1+2.yn2+2.yn3+yn4)
Conclusion
Comme on peut le constater, la méthode de Runge-Kutta (d'ordre 4) est assez ardue;
cependant, le gain de rapidité est important.
Pour ces deux raisons, nous allons principalement employer cette méthode dans les
programmes qui nécessitent le plus de ressources ; pour d'autres, nous lui préfèrerons la
méthode d'Euler améliorée.