Exercice 27: Pythagore, Thalès ,trigonométrie

1
CORRECTION Exercice 27 : Pythagore, Thalès ,trigonométrie
agrandissement
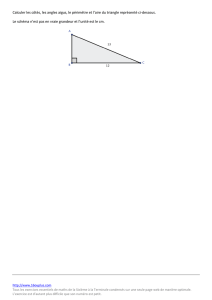
L’unité de longueur est le centimètre. Tracer un segment [AB] tel que AB = 12.
Placer le point H du segment [AB] tel que AH = 1.
Tracer ensuite un demi-cercle de diamètre [AB] et la perpendiculaire en H à la droite (AB).
On note C le point d’intersection de cette perpendiculaire avec le demi-cercle.
a. nature du triangle ABC
On sait que [AB] est un diamètre du cercle ( C ) et que le point C est sur ce cercle
Or si un triangle a pour sommets les extrémités d’un diamètre et un point du cercle alors c’est un triangle
rectangle en ce point
Donc ABC est un triangle rectangle en C
b. Exprimons de deux façons le cosinus de l’angle BÂC puis calculons AC
Dans le triangle ABC rectangle en C, exprimons cos BÂC
Cos BÂC =
12
AC
AB
AC 
 Dans le triangle CAH rectangle en H, exprimons cos CÂH ( CÂH = CÂB)
Cos BÂC =
AC
1
AC
AH 
On en déduit
AC
1
12
AC 
, d’où AC² = 12
Comme AC est une longueur , on en déduit AC =
12
=
323232  ²²
AC =
32
c . calculons la mesure arrondie au degré de l’angle BÂC.
Dans le triangle ABC rectangle en C
Cos BÂC =
6
3
1232 
BÂC = cos
6
3
1
; BÂC  73°
d ; Après avoir placé le point D de la droite (BC) tel que B, C et D soient dans cet ordre et
que CD = 6.
 Calculons la valeur exacte de la longueur AD
Dans le triangle ACD rectangle en C, d’après le théorème de Pythagore
AD² = AC² + CD²
AD² =
2
2632 
AD² = 4  3 + 36
AD² = 12 + 36
AD² = 48
AD =
3432232248 22 
AD =
34
 Calculer la mesure, en degrés, de l’angle ADC.
Dans le triangle ADC rectangle en C. utilisons le sinus de l’angle ADC
Sin ADC =
2
1
34
32
AD
AC 
ADC = 30°

2
e. Après le point E du segment [AD] tel que AE = 2 et le point F du segment [AC] tel que
AEF = 30° puis
 prouvons que les droites (EF) et (DC) sont parallèles.
On sait que ADC = AEF = 30°
Ces deux angles sont construis avec deux droites (DC) et (EF) coupées par une sécante (AD) ; ils
sont donc correspondants
Or deux angles correspondants égaux déterminent des droites parallèles
Donc (DC) // (EF)
 Calculons la longueur AF.
On sait que (DC) // (EF) ; E  [AD] et F  [AC]
Les triangles ainsi formés AEF et ADC ont leurs côtés correspondants proportionnels d’après le
théorème de Thalès d’où
DC
EF
AC
AF
AD
AE 
;
6
EF
32
AF
34
2
;
32
AF
34
2
28 On sait que
AF =
34
322
; AF = 1 cm
AB H
C
D
EF