1) Cours

Page 1 / 6
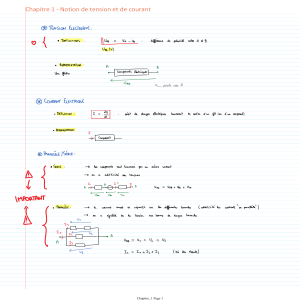
1) Cours
- Rappeler les lois de Kirchhoff
- Définir densité de courant (volumique, surfacique, linéique).
- Loi d’ohm locale et intégrale.
2) K représente un interrupteur fermé, R une résistance.
L’interrupteur est supposé parfait :
-la chute de tension à ses bornes est nulle lorsqu’il est
fermé.
- le courant qui le traverse est nul lorsqu’il est ouvert.
On donne u (t) et l’état de K en fonction
du temps :
Tracer uK (t) et u R (t) en concordance de temps avec u (t).
3)
Exprimer I1 en fonction de I0, R1 et R2.
4)
Exprimer U en fonction de E, r et R.

Page 2 / 6
5) Soit une diode à jonction, dont la caractéristique est la suivante
On place cette diode dans un circuit comportant un générateur linéaire et une résistance. Le
générateur est une source de courant pure (noté ).
5.1) Exprimer I circulant dans R quand  varie (distinguer deux cas, diode « bloquée » et
diode « passante »).
5.2) L’intensité maximale supportée par R est 10 mA. Quelle valeur maximale positive  max
peut prendre ?
6) Etude d’un réseau (ci-contre)
Etablir l’expression de U en utilisant :
6.1) les lois de Kirchhoff
6.2) le théorème de superposition
7) Pour une résistance non-linéaire (RNL), on a mesuré :
i (en mA)
10
20
30
40
45
50
55
60
65
U (en V)
4
10
20
33
42
52
65
80
100
7.1) Cette résistance non-linéaire est mise en série avec une résistance linéaire R = 1000 .
L’ensemble est soumis à une tension de 100 V.

Page 3 / 6
Déterminer l’intensité du courant dans ce montage et la tension aux bornes de chacun des
dipôles.
7.2) On réalise maintenant l’association en parallèle et la tension appliquée aux bornes de
l’association est de 60 V. Déterminer i R et i RNL
8) Cours :
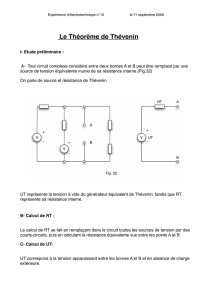
- Théorèmes de Thevenin et de Norton (lien entre les deux ?)
- Théorème de superposition
9) Exemple de groupements
Déterminer les paramètres du dipôle équivalent au groupement des générateurs représentés ci-
dessous entre A et B :
10) Soit le montage suivant :
Calculer les courants i1 à i5.
10.1) En appliquant les lois de Kirchhoff
10.2) Par Thévenin et/ou Norton
On donne :
R1 = 10  ; R2 = 2  ; R3 = 3  ; R4 = 5  ; R5 = 2  ; E1 = 100 V ; E2 = 50 V ; E3 = 50 V.

Page 4 / 6
11) Soit le montage suivant :
11.1) Transformer les sources de courant (i1, r1) et (i2, r2) en sources de tension.
11.2) Calculer, par la méthode de votre choix, les courants I4 et I5.
12) On considère le montage suivant :
Calculer i en utilisant le théorème de superposition.
13) On donne : E1 = 12 V ; E2 = 6 V ; R0 = 20  ; R1 = 10  ; R2 = 4  .
13.1) Déterminer le modèle équivalent de Norton du dipôle qui alimente R.
13.2) Calculer i si R = 5 
14) Pour le circuit suivant, trouver le courant dans R :
14.1) Par Norton (exclusivement)
14.2) Par Thévenin (exclusivement)
14.3) Par superposition
14.4) Par les lois de Kirchhoff
14.5) Expliquer pourquoi il n’est pas
possible d’utiliser le théoorème de Millman
pour résoudre ce problème.

Page 5 / 6
15) Cours :
 Théorème de Millman (démonstration demandée).
 Théorème de Kennely.
16) Applications
on suppose qu’il y a équivalence entre les deux montages suivants :
16.1) Préciser le sens du mot « équivalence ».
16.2) Calculer
R
R
R
A
B
C
en fonction de RAB , RAC et RBC .
16.3) A.N. : RAB = RAC =10  RBC = 12 . ; VA = + 2,5 V = VB ; VC = - 5 V
Calculer RA , RB et RC .
En utilisant le théorème de Millman, calculer VN.
17)
Quel est le modèle équivalent de
Thévenin vu entre les bornes A et B ?