exerc2

Solutions
È
Cours
È
2.1 – Lois des mailles
Calculer l’intensité dans chacune des branches de ce circuit.
E1
R3
R2
R1
R5
R4
E1 = 8 V ; E2 = 12 V.
E3 = 6 V ; E4 = 2 V.
R1 = R2 = 5 Ω.
R3 = R4 = R5 = 10 Ω.
E2
E3
E4
2.2 – Lois des mailles
Calculer l’intensité dans chacune des branches de ce circuit.
R1
R2
R5
R4
E1
E1 = 6 V ; E2 = 12 V.
R1 = R5 = 20 Ω.
R3 = R4 = 40 Ω.
R2 = 10 Ω
R3
E2
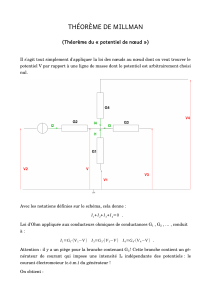
2.3 – Principe de superposition
Calculer U et I en utilisant :
– la loi des mailles,
– le principe de superposition,
– le théorème de Millman.
E1 = 10 V ; E2 = 40 V.
R1 = 5 Ω ; R2 = R3 = 10 Ω.
A
C
R1
R2
I
U
E1
E2
R3
2.4 – Générateurs équivalents
E est un générateur de tension idéal (E = 12 V)
R1
I
R1 = 2 kΩ ; R2 = 1 kΩ
Calculer le courant dans la résistance de charge RC et la
Rc
R2
tension entre ses bornes si : RC = 0 Ω, 500 Ω, 1 kΩ, 2 kΩ,
E
100 kΩ. Conclusions.
Reprendre cet exercice en utilisant un générateur de Thévenin équivalent.
2.5 – Générateurs équivalents
Chercher les générateurs de Thévenin et de Norton équivalents à ces trois circuits.
a) I1 = 5 A, I2 = – 2 A, R1 = 10 Ω, R2 = 20 Ω.
b) E = 4 V, I2 = 1 A, R1 = R2 = 10 Ω.
c) E1 = – 4 V, E3 = 2 V, I1 = 1 A, R1 = R2 = R3 = 10 Ω.
E
R1
E1
R2
I1
I1
R1
–a–
R2
I2
R1
R2
–b–
R3
E3
I2
–c–
2.6 – Générateurs équivalents
Reprendre l’exercice 2.3 en utilisant les générateurs de Thévenin et de Norton équivalents.
2.7 – Droite de charge
Reprendre l’exercice suivant en utilisant un générateur de Thévenin équivalent.
U (V)
Une lampe à incandescence L a la
10
caractéristique ci-contre.
R1
Elle est alimentée par le circuit dont les
éléments valent :
R2
5
E
E = 20 V ; R1 = R2 = 2 kΩ.
L
Déterminer le courant qui circule dans la
I(mA) lampe et la tension entre ses bornes.
5
10
2.8 – Pont de Wheatstone déséquilibré
On considère un pont de Wheatstone dont la résistance du bras détecteur est RC.
D
Calculer le courant qui circule dans la résistance RC. On
R1
donne :
R3
E
Rc
E=6V;
R1 = R2 = 3 kΩ.
A
B
R3 = 2 kΩ.
R4 = 1 kΩ.
R4
R2
M
2.9 – Théorème de Kennelly
Montrer l’équivalence des deux circuits en exprimant les résistances de l’étoile en fonction
de celles du triangle et réciproquement.
R 23
2
2
3
R12
3
R3
R13
1
R2
R1
Triangle
1
Etoile
2.10 – Simplification de circuit
R1
R2
E
Calculer le courant qui circule dans la résistance RC.
On pourra utiliser la transformation étoile-triangle ou
mieux le théorème de Thévenin.
I
R3
R4
RC
R5
2.11 – Simplification de circuit
R3
E
R2
R1
R2
R1
R2
R1
R2
I
R1
RC
Calculer le courant qui circule dans la
résistance RC.
On donne :
E = 18 V.
R1 = 4 kΩ.
R2 = 3 kΩ.
R3 = 6 kΩ.
2.12 – Convertisseur digital-analogique
Les tensions appliquées sont E.ki avec :
E
k1
k2
k3
k4
ki = 0 si l’inverseur est relié à la masse.
ki = 1 si l’inverseur est relié à E.
2R
2R
2R
2R
En utilisant le théorème de Millman en A, B, C et D,
A
montrer que :
D
R B
R C R
kE kE kE kE
2R
VS = 1 + 2 + 3 + 4
16
8
4
2
2.13 – Simplification de circuit
A
Déterminer (en fonction de R) la valeur de r pour
laquelle la résistance présentée par le circuit entre A et
B est égale à R.
Il est conseillé de modifier le schéma initial.
r
r
r
E
R
r
B
2.14 – Stabilisateur de tension
La tension aux bornes d’une thermistance en fonction du courant est la suivante :
0
4
6,5
8,2
8,6
9
8,7
8
i (mA)
0
5
10
20
25
35
65
100
I
i
u
E = 24 V
ut
Solutions
È
Th
Rc = 800Ω
r = 15 Ω
R
ut (V)
On considère le circuit ci-contre.
a) Tracer u = f ( i ).
b) Exprimer u = g(E, i, R, RC)
c) Calculer R pour avoir un courant i égal à 60 mA.
d) Déterminer la variation de u quand la tension E
varie de ± 15 %.
Retour au menu
È