Simplifier les fractions suivantes sous forme de fractions irréductibles

Quatrième – 4800 – Fractions - Simplifications – 17.05.12
http://www.soutienpedagogique.com
Simplifier les fractions suivantes sous forme de fractions irréductibles:
Méthode - Ce qu’il faut avoir assimilé pour résoudre ces exercices:
Savoir décomposer les numérateurs et dénominateurs en produit de facteurs premiers.
Simplifier la fraction supprimant les facteurs communs au numérateur et au dénominateur.
Une fraction est irréductible dès lors qu’elle possède un nombre premier au numérateur ou au
dénominateur.
Les nombres premiers sont divisibles par 1 ou par eux-mêmes : 1,2,3,5,7,11,13,17,19,23,29,31….
Les nombres pairs sont divisibles par 2.
Si la somme des chiffres qui composent un nombre est divisible par 3, alors le nombre est divisible
par 3.
Si le chiffre des unités d’un nombre est 0 ou 5, le nombre est divisible par 5.

Quatrième – 4800 – Fractions - Simplifications – 17.05.12
http://www.soutienpedagogique.com
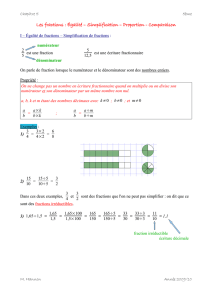
On décompose le numérateur et le dénominateur en produits de facteurs premiers et on simplifie.
On décompose le numérateur et le dénominateur en produits de facteurs premiers. Dans ce cas, il ne
sert à rien de décomposer totalement le dénominateur en produit de facteurs premiers car, après
simplification, il rest un 1 au numérateur qui est un nombre premier :
On décompose le numérateur et le dénominateur en produits de facteurs premiers et on simplifie.
On décompose le numérateur et le dénominateur en produits de facteurs premiers. Dans ce cas, il ne
sert à rien de décomposer totalement le dénominateur en produit de facteurs premiers car, après
simplification, il rest un 1 au numérateur qui est un nombre premier :
75 est divisible par 3 et 5, 35 est divisible par 5 mais pas par 3. On fait apparaître le 5 dans la
décomposition en produits de facteurs sans décomposer totalement.
7 étant un nombre premier, même si 15 est encore divisible par 3 et 5, la fraction est irréductible.

Quatrième – 4800 – Fractions - Simplifications – 17.05.12
http://www.soutienpedagogique.com
On décompose le numérateur et le dénominateur en produits de facteurs premiers et on simplifie.
On décompose le numérateur et le dénominateur en produits de facteurs premiers et on simplifie.
5 et 23 étant des nombres premiers, la fraction est irréductible.
On décompose le numérateur et le dénominateur en produits de facteurs premiers et on simplifie.
7 étant un nombre premier, même si 58 est encore divisible par 2, la fraction est irréductible.