D1_b_Activités suppl_Suites et séries_3A_2014

P.S. 2014-2015 1 Activités Suites et séries 3A
Travaux supplémentaires : suites et séries
Résoudre un des problèmes proposés ci-dessous.
Titre du travail de groupe :
Noms
des élèves :
(max. 2 élèves)
Date de
présentation : Notes :
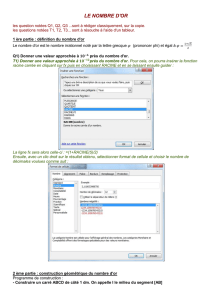
01) Découverte de la suite Fn
de Fibonacci trois activités à
traiter simultanément.
02) Dérivation géométrique de
l’équation pour Φ (Phi)
Deux activités à traiter en
parallèle. Φ est le nombre d’or.
03) Découvrir la formule de
Binet :
()
()
n
n
n
1
F5 =Φ−Φ
04) Limite de Fn / Fn-1.
Prouver que si n → ∞ alors
Fn/ Fn-1 → Φ
05) Découvrir la courbe
de Von Koch
Notion de fractale
06 ) Découvrir la spirale d’or
07 ) Le calcul de
π
par la
méthode d’Archimède
08 ) Le binôme de Newton
09 ) Dosage de chlore
10 ) Capital à intérêts
composés et valeur de l’annuité

P.S. 2014-2015 2 Activités Suites et séries 3A
Indications pour les travaux de groupes :
• Présentation :
a) Manuscrite sur des feuilles A4.
b) L’énoncé des exercices doit faire partie de la présentation.
b) Ecrire lisiblement au stylo (mais pas rouge).
• Critères d'évaluations :
a) Autonomie dans la recherche des solutions.
b) Pertinence des réflexions, résultats.
c) Clarté, présentation.
d) Présentation orale.
• Durée de présentation :
a) 30 minutes au maximum.
b) Chaque élève doit présenter oralement une partie du travail.

P.S. 2014-2015 3 Activités Suites et séries 3A
Travail de groupe 01
Découverte de la suite Fn de Fibonacci
a) Enoncé : Les faux-bourdons.
Indications
L’arbre généalogique
Un arbre généalogique ascendant représente tous les ancêtres d’un individu.
On place cet individu au bas de la feuille, et on dessine les deux branches qui le relient à ses
parents. Les parents sont représentés selon leur sexe :
pour le père
pour la mère
On continue l’arbre en représentant les parents des parents, et ainsi de suite.
(Toutes les personnes d’une même génération sont dessinées au même niveau).
La reproduction chez les abeilles
La population des abeilles comporte trois sortes d’individus :
- La reine, seule femelle féconde.
- Les faux-bourdons, qui sont les mâles.
- Les ouvrières, qui sont des femelles stériles.
La reine s’accouple au printemps avec des faux-bourdons et a ensuite la faculté de pondre deux
sortes d’œufs :
- Des œufs fécondés d’où naîtront des femelles, reine ou ouvrières.
- Des œufs non fécondés d’où naîtront des faux-bourdons.
On peut en conclure que les abeilles femelles ont deux parents, alors que les faux-bourdons n’ont
pas de père !
Question
Avec les informations ci-dessus, trouver le nombre maximum des ascendants d’un faux-bourdon
à la 1ère, 2ème, 3ème, 4ème, 5ème et 6ème , ……… et 12ème génération ?
Indication :Le dessin de l’arbre généalogique peut aider à répondre aux questions précédentes.
b) Enoncé : Les lapins de Fibonacci.
Énoncé du XIIe Siècle
« Combien de couples de lapins obtiendrons-nous à la fin d'une année si,
commençant avec un couple, chacun des couples produit chaque mois
un nouveau couple, lequel devient productif au second mois de son existence ? »
Énoncé actualisé
Si, dès que les deux lapins d’un couple sont âgés de deux mois, ce couple engendre chaque mois
un nouveau couple de lapins, trouver combien il y aura de couples de lapins au bout d’une année.
Indication : en partant d’un couple né début janvier, déterminer le nombre de couples de lapins
qu’il y aura en janvier, février, mars, avril, mai, juin, …… et décembre.

P.S. 2014-2015 4 Activités Suites et séries 3A
Compléments sur la suite de Fibonnacci
• Qui est Fibonacci ?
De son vrai nom Léonard de Pise, Fibonacci est né en Italie, plus précisément à Pise en 1175. Il
décède en 1240 à l’âge de 65 ans. Dans sa jeunesse, il apprend les bases de l’arithmétique dans sa
ville natale. Fils de marchand, il voyage beaucoup avec son père, ce qui lui permet de lire les
écrits de plusieurs mathématiciens arabes tel que, Al Khwarizmi, qui fut le premier à utiliser le
système algébrique. Par la suite, il fit plusieurs autres voyages autour de la mer Méditerranée lors
desquels il étudia le système de numération indienne et les différents systèmes de calculs
pratiqués en Orient. Lorsqu’il revint de ses voyages, il décida de publier un livre, Liber abbaci,
qui parle des méthodes arabes en mathématique, qui permettront un progrès important des
mathématiques et notamment de l’algèbre. En 1220, Fibonnaci sort un autre livre, intitulé Patrica
geometriae, qui regroupe toutes les connaissances de l’époque en géométrie et en trigonométrie.
En plus de faire parvenir à l’Europe les connaissances orientales et ancestrales mathématiques,
Fibonacci poursuit ses propres travaux. Bien évidemment c’est Leonard de Pise qui présenta la
fameuse « suite de Fibonacci ». C’est grâce à une étude sur la reproduction des lapins qu’il
parvient à mettre en place cette suite.
Léonard de Pise dit Fibonacci
• Définition :
Les nombres de Fibonacci forment une suite de nombres que l'on appelle suite de Fibonacci.
Un nombre de la suite s'obtient en ajoutant les deux nombres précédents de la suite :
Si on note Fn le nème nombre de Fibonacci, Fn = Fn - 1 + Fn - 2
Voila les premiers nombres de la suite : F1 = 1 ; F2 = 1 ; F3 = 2 ; F4 = 3 ; ...etc
indice n 1 2 3 4 5 6 7 8 9 10 11 ... ...
Fn 1 1 2 3 5 8 13 21 34 55 89 ... ...

P.S. 2014-2015 5 Activités Suites et séries 3A
Le nom de suite de Fibonacci a été donné par l'arithméticien français Edouard Lucas en 1817,
alors qu'il étudiait ce qu'on appelle aujourd'hui les "suites de Fibonacci généralisées" obtenues
en changeant les deux premiers termes de la suite de Fibonacci et qui suivent le même procédé de
construction.
La plus simple d'entre elles, dont les deux premiers termes sont 1 et 3, s'appelle aujourd'hui ... la
suite de ... Lucas ! (Elle commence par 1, 3, 4, 7, 11, 18, 29, 47, ...). Les suites de Fibonacci et de
Lucas sont très liées.
• Quelques résultats mathématiques sur les nombres de Fibonacci et de Lucas :
On note (Fn) la suite de Fibonacci définie par Fn = Fn - 1 + Fn - 2 ; F1 = 1 et F2 = 1 .
On note (Ln) la suite de Lucas définie par Ln = Ln - 1 + Ln - 2 ; L1 = 1 et L2 = 3 .
On note (Gn) une suite de Fibonacci "généralisée" définie par Gn = Gn - 1 + Gn - 2 sans préciser les
valeurs de G1 et G2 .
Voici quelques résultats intéressants.
1. Fn2 = Fn-1 Fn-2 + e , où e = 1 ou -1
2. Gn2 = Gn-1 Gn-2 + e (G22 - G12 - G1G2) , où e = 1 ou -1
3. Fn2 + Fn+12 = F2n+1
4. Fn+22 - Fn+12 = Fn Fn+3
5. Ln = Fn-1 + Fn+1
6. FnLn = F2n
7. Pour tout entier n, il existe une infinité de nombre de Fibonacci divisibles par n.
8. Pour tout entier n, il existe un nombre de Fibonacci divisible par n, parmi les 2n premiers
termes de la suite.
9. Pour tout entier n différent de 3, si Fn est un nombre premier alors n est un nombre premier.
La réciproque est fausse ! F19 = 4181 = 37 x 113 est le plus petit contre-exemple.
On ne sait pas s'il existe une infinité de nombres premiers parmi les nombres de Fibonacci.
10. Pour tout entier n différent de 3, si n n'est pas un nombre premier alors Fn n'est pas un
nombre premier.
(Formulation contraposée de la proposition précédente)
11. F12 = 144 est la seul carré parfait de la suite de Fibonacci (à part les triviaux F1 = 1 et F2 =
1)
12. Fm+n = Fm+1Fn + FmFn-1
13. si m divise n alors Fm divise Fn
14. PGCD (Fn ; Fn+1) = 1 pour tout n
15. PGCD (Fm ; Fn) = FPGCD(m ; n)
La proposition 15 est fascinante !
Elle affirme que le PGCD de deux nombres de Fibonacci est aussi un nombre de Fibonacci et
que, de plus, ce n'est pas n'importe lequel...