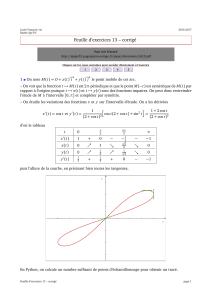
Proposition : La suite (Llog 2(n)C) est 2

Le but du pr´esent article est de d´emontrer que la suite (b1
2+log2(n)c) n’est pas une
suite 2-rationnelle. On commence par rappeler les outils dont on aura besoin.
Proposition : La suite (blog2(n)c) est 2-rationnelle.
D´emonstration : On a, pour tout n entier naturel:
blog2(2n)c= 1 + blog2(n)c
blog2(2n+ 1)c= 1 + blog2(n)c
(Il s’agit de la longueur de l’´ecriture binaire de n)
Proposition : Une suite enti`ere born´ee est k-automatique si et seulement si
elle est k-rationnelle
D´emonstration : Admis.
Ainsi, on est ramen´e au probl`eme suivant : d´emontrer que (b1
2+log2(n)c −
blog2(n)c)nn’est pas une suite 2-automatique (les suites 2-rationnelles forment
un anneau avec l’addition et le produit de convolution usuels) Enfin, faisons la
remarque suivante:
bx+1
2c−bxc= 0 ⇔ ∃k∈N, k ≤x<k+1 2
Soit
blog2(n) + 1
2c−blog2(n)c= 0 ⇔ ∃k∈N,2k≤x < 2k√2
Par l’absurde, on suppose que (un)=(blog2(n) + 1
2c−blog2(n)c) est une suite
2-automatique. Alors (un+1) est 2-automatique (r´esultat classique).
On prend les deux AFDS associ´es `a (un),(un+1):
(Q1,{0; 1},{0; 1}, δ1, q0, τ1),(Q2,{0; 1},{0; 1}, δ2, q0
0, τ2)
On construit alors l’automate produit muni de la fonction de sortie suivante :
τ(q) = 1 si τ1(q) = 0 et τ2(q) = 1 Les nombres tels que (vn) soit ´evalu´ee `a 1 sont,
d’apr`es la remarque pr´eliminaire, les nombres n tels que:
n < 2k√2≤n+ 1
soit n=b2k√2cPosons le langage, rationnel par hypoth`ese:
{w∈ {0; 1}∗; [w]2=b2k√2c}
Ce langage est totalement ordonn´e pour la relation pr´efixe, de limite l’´ecriture
binaire de √2. D’apr`es le lemme de l’´etoile, le mot infini limite de ce langage
est p´eriodique `a partir d’un certain rang. Autrement dit, √2 est rationnel. Con-
tradiction et r´esultat. Cette m´ethode peut se g´en´eraliser aux suites de la forme
(bα+logk(n)c) qui ne sont pas k-rationnelles si et seulement si kαest irrationnel.
1