1) Fonction reciproque 2) Propriete de la fonction

Exposé 65 : Fonction reciproque d’une fonction continue strictement monotone sur un
intervalle de . Exemple.
Pre requis :
- notion d’intervalle
- bijection
- continuité et derivabilité d’une fonction
- theoreme des valeurs intermediaires
dans tout l’exposé, I designe un intervalle non vide de
. On note
( )
m
C I
l’ensemble des
fonctions continues et strictement monotones sur I.
1) Fonction reciproque
Theoreme : Si
( )
m
f C I
∈ alors f realise une bijection sur
( )
f I
Preuve :
( )
f I
est un intervalle d’apres le theoreme des valeurs intermédiaires
: ( )
f I f I
→
est surjective par construction
Soit
2
1 2
( , )
x x I
∈
, supposons
f
strictement croissante (on change le sens des inegalité si elle
est strictement decroissante, ou on considere
f
−
qui sera alors strictement croissante)
1 2 1 2
( ) ( )
x x f x f x
< ⇒ < donc
f
injective.
Definition : Soit
( )
m
f C I
∈. L’application qui a tout
( )
y f I
∈
associe son unique antecedent
par la fonction
f
est appelée fonction reciproque de
f
. On la note
1
f
−
Remarque :
1
( )
( )
( )
y f x
x f y
x I
y f I
−
=
=
  ⇔
∈∈
Si
( )
m
f C I
∈ alors
1
I
f f Id
−
= et
1
( )
f I
f f Id
−
=
Preuve (si le jury le demande)
, ( )
x I y f I
∈ ∈
tel que
1
( ); ( )
y f x x f y
−
= =
1 1 1
( ) ( )
I
f f x f y x f f Id
− − −
= = ⇒ =
2) Propriete de la fonction reciproque
a) Sens de variation
Proposition : Si
( )
m
f C I
∈ alors
1
f
−
est strictement monotone sur
( )
f I
et a le même sens de
variation que
f
.

Preuve : cas où
f
est strictement croissante sur I
Soient
2
1 2
( , ) ( ( ))
y y f I
∈ tel que
1 2
y y
<
. On pose
1 1 2 2
( ), ( )
x f y x f y
= =
1 1
1 2 1 2 1 2 1 2
( ) ( ) ( ) ( )
y y f x f x x x f y f y
− −
< ⇒ < ⇒ < ⇒ <
L’implication du milieu vient du fait que
f
est croissante donc
1 2 1 2
( ) ( )
x x f x f x
< ⇒ < or si
on prend la contraposé on a
2 1 2 1
( ) ( )
f x f x x x
≤ ⇒ ≤
.
b) Continuité
Lemme : Soit
( )
m
f C I
∈.
( )
f I
est un intervalle si et seulement si
f
est continue sur I.
Preuve : cela vient du fais que l’image d’un compact par une fonction continue est un
compact.
Propriété : Si
( )
m
f C I
∈ alors
1
f
−
est continue sur
( )
f I
.
Preuve ( à faire) :
f
est continue et strictement monotone sur I donc
f
est bijective de I sur
( )
f I
.
f
continue implique
( )
J f I
=
est un intervalle, or
1
f
−
existe et est strictment monotone d’où
1
( )
f J I
−
=
, intervalle, ce qui entraine
1
f
−
continue.
Exemple :
[ ]
, 1,1
:2 2
sin
f
x x
π π
− → −
c) Dérivabilité
Theoreme : Soit
( )
m
f C I
∈ et
o
x I
∈
tel que
f
soit derivable en
o
x
et
'( ) 0
o
f x
≠
Alors
1
f
−
est dérivable en
( )
o o
y f x
=et on a
1
1
1 1
( ) '( )
'( ) '( ( ))
o
o o
f y
f x f f y
−
−
= =
Remarque : il se peut que
f
ne soit pas derivable en un point et que
1
f
−
le soit. Sur le graphe
,
f
aura une tangente verticale, et donc
1
f
−
une tangente horizontale.
Preuve (du theoreme) :
Montrons que
1 1
( ) ( ) 1
lim , '( ) 0
'( )
o
o
o
y y o o
f y f y f x
y y f x
− −
→
−
= ≠
−
La fonction
f
étant dérivable en
o
x
, on a
( ) ( )
'( ) lim
o
o
ox x o
f x f x
f x x x
→
−
=−, comme
1
f
−
est
continue en
o
y
, le théoreme de compositions de limites donne :

1
1 1 1
( ( )) ( )
'( ) lim lim
( ) ( ) ( )
o o
o o
ox x y y
o o
f f y f x y y
f x
f y x f y f y
−
− − −
→ →
− −
= =
− −
Cette limite etant supposée non nulle, d’apres le theoreme de l’inverse d’une limite,on a (en
fait c’est le theoreme des compositions de fonction avec la fonction inverse, sur un point non
nul donc ou la fonction onverse est definie)
1 1
( ) ( ) 1
lim , '( ) 0
'( )
o
o
o
y y o o
f y f y f x
y y f x
− −
→
−
= ≠
−
Exemple :
2 2
1 1 1
(arctan ) '
1 1 tan (tan ) '
tan
arctan
x
x y y
y x
y x
= = =
+ +
=
=
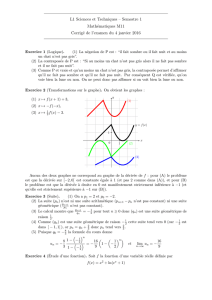
d) Graphe
Soit
( )
m
f C I
∈
Graphe de
f
:=
{
}
( , ( );
f
G x f x x I
= ∈
Graphe de
1
f
−
:=
{
}
{
}
1
1
( , ( )); ( ) ( ( ), );
f
G y f y y f I f x x x I
−
−
= ∈ = ∈
1
f
G
−
est donc le symetrique de
f
G
par rapport à la 1
ere
bissectrice
Dessin
3) Exemple
a) Fonction exponentielle et logarithme neperien.
exp :
∗
+
→ exp est continue et strictmenent monotone sur
exp( )
∗
+
=
Elle admet une fonction reciproque qui est ln :
∗
+
→
( , ) ( , ln )
x
x e y y x y
∗
+
∀ ∈ = ⇔ ∀ ∈ =
dessin
b) Fonction tangente et arctangente
tan : ,
2 2
π π
− →
, tan est continue et strictement monotone sur cet intervalle.

tan ,
2 2
π π
− =
, elle admet donc une fonction reciproque notée arctan.
arctan : ,
2 2
π π
→ −
( )
, , tan ,arctan
2 2
x x y y y x
π π
∀ ∈ − = ⇔ ∀ ∈ =
dessin