(Voir 4ème, chapitre 11.) I) Angles et cercle Définitions : Dans un

3ème – Ch. 12
© 2008-2009 easymaths.free.fr Page 1 sur 4
(Voir 4ème, chapitre 11.)
I) Angles et cercle
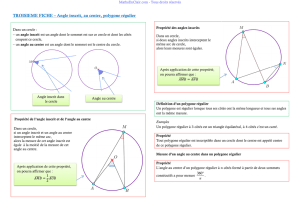
Définitions :
Dans un cercle,
• Un angle intercepte un arc de cercle
p
A
B si ses côtés sont sécants avec le cercle
aux points A et B.
• Un angle inscrit est un angle formé par deux cordes issues d’un même point du
cercle.
(Ou aussi, angle dont le sommet est sur le cercle et dont les côtés coupent ce
cercle.)
• Un angle au centre est un angle dont le sommet est le centre du cercle.
Exemples :
A, M et B sont trois points distincts d’un cercle C de centre O.
• Cas où
n
AMB aigu. (M et O du même côté de la corde [AB].)
M
N
A
B
C
O
arc interce
p
téL'
+
L’angle
n
A
MB est un angle inscrit dans C qui
intercepte le petit arc
p
A
B.
L’angle
n
AOB est un angle au centre dans C
qui intercepte le même arc
p
AB . C’est l’angle
au centre associé à l’angle inscrit
n
AMB .
• Cas où
n
A
MB obtus.
M
A
B
C
O
+
n
A
MB et AOB interceptent le grand arc
p
A
B.
Contre-exemples :
Les angles ci-contre sont ni inscrits,
ni au centre !
O
+
CHAPITRE 12 Angles et cercle. Polygones réguliers.

3ème – Ch. 12
© 2008-2009 easymaths.free.fr Page 2 sur 4
Propriétés :
Dans un cercle,
• Si un angle au centre et un angle inscrit interceptent le même arc, alors la
mesure de l’angle inscrit est égale à la moitié de celle de l’angle au centre.
• Si deux angles inscrits interceptent le même arc, alors ils ont la même mesure.
Exemples :
n n
1
2
AMB AOB= et
n
n
AMB ANB=
Propriété : (Rappel de 4ème : cas où [AB] est un diamètre.)
Si le cercle circonscrit à un triangle AMB a pour diamètre [AB], alors AMB est
rectangle en M. (1/2 de 180°.)
II) Polygones réguliers
A) Définition, propriétés
Définition :
Un polygone est dit régulier si tous ses côtés ont la même longueur et tous ses
angles (« au sommet ») ont la même mesure.
Exemples et contre-exemple :
• Un triangle équilatéral est un polygone régulier à trois côtés.
• Un carré est un polygone régulier à quatre côtés.
• Un losange n’est pas un polygone régulier : ses côtés ont la même longueur mais
ses angles n’ont pas la même mesure !
Propriété et définitions :
• Il existe un cercle passant par tous les sommets d’un polygone régulier, le cercle
circonscrit au polygone.
• Le centre de ce cercle est appelé centre du polygone régulier.
Propriété :
Un polygone est régulier s’il est inscriptible dans un cercle et que tous ses côtés ont
la même longueur.
Propriété et définition : (Invariance)
A et B désignent deux sommets consécutifs d’un polygone régulier de centre O. La
rotation de centre O et d’angle
n
AOB transforme le polygone régulier en lui-même.
On dit que le polygone est invariant par cette rotation.
Conséquences :
• Un polygone régulier (non croisé) à n côtés est invariant par une rotation autour
de son centre, d’angle 360 n°.
• La mesure de l’angle au centre interceptant un des côtés est égale à 360 n°.
• Tous les angles « au centre » d’un polygone régulier ont la même mesure.
Vocabulaire :

3ème – Ch. 12
© 2008-2009 easymaths.free.fr Page 3 sur 4
Une figure est dite invariante par une transformation si chaque point de cette figure a
pour image un point de la figure par cette transformation.
B) Constructions (Polygones réguliers à 3, 4 ou 6 côtés)
Construire le polygone régulier de centre O dont le point A est un sommet.
• Triangle équilatéral :
Il est sa propre image par la rotation de centre O et d’angle 360 3 120°= °.
Méthode 1 : (rapporteur)
Construire C, image de A par la rotation
de centre O et d’angle 120°, puis
l’image E de C par cette rotation.
+
A
O
C
E
120°
120°
Méthode 2 : (compas)
Placer sur le cercle les points B, C, D et
E tels que OA = AB = BC = CD = DE, et
« prendre un point sur deux ».
+
A
O
C
E
B
D
O est le « centre » de ABC mais ABC n’a pas de centre de symétrie !
• Carré :
Il est sa propre image par la rotation de centre O et d’angle 360 4 90°= °.
Méthode 1 : (rapporteur)
Par la rotation de centre O et d’angle
90°, construire l’image B de A, puis
l’image C de B et enfin l’image D de C.
+
O
D
CB
A
90°
+
Méthode 2 : (équerre)
Tracer deux diamètres [AC] et [BD]
perpendiculaires.
+O
D
CB
A+
• Hexagone régulier :
Il est sa propre image par la rotation de centre O et d’angle 360 6 60°= °.
Méthode 1 : (rapporteur)
Construire B, image de A par la rotation
de centre O et d’angle 60°, puis l’image
C de B par cette rotation, etc.
Méthode 2 : (compas)
Placer sur le cercle les points B, C, D, E
et F tels que OA = AB = BC = … = EF.

3ème – Ch. 12
© 2008-2009 easymaths.free.fr Page 4 sur 4
+A
O
B
C
D
E
F
60°
120°
+A
O
B
C
D
E
F
n
180 60BCD =°−°