01TTP Approximation lineaire

§0 Rappels sur fonctions et graphes
Une fonction f définie sur un intervalle I de
ℝ
permet de faire correspondre à tout élément de I un
réel. On appelle graphe de f l’ensemble des points
(
)
(
)
,
x f x
dans le plan muni d’un repère. Les
nombres
(
)
f x
pour
x I
∈
sont les valeurs de f .
Un maximum de f est un réel égal à une valeur de f , soit
(
)
0
f x
, et telle que pour tout autre élément
x de I , on ait
(
)
(
)
0
f x f x
≤ . On définit de même la notion de minimum, et de maximum et
minimum relatifs. L’existence de maximum et de minimum dépend de la fonction et de l’intervalle.
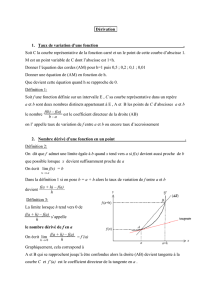
La dérivée d’une fonction f en un point
0
x
est la limite lorsque x tend vers
0
x
du taux
d’accroissement
(
)
(
)
0
0
f x f x
x x
−
−. Ce dernier est le coefficient directeur de la corde du graphe
joignant les points d’abscisses x et
0
x
. On sait que la dérivée de f en
0
x
, que l’on note
(
)
0
f x
′
est le
coefficient directeur de la tangente au graphe de f en
0
x
. La dérivée permet aussi d’indiquer le sens
de variation de la fonction f par l’étude de son signe, elle permet par voie de conséquence de
déterminer, s’ils existent, les extremums.
On peut grâce à cela calculer l’équation de la tangente au graphe de f en
0
x
qui est donnée par
(
)
(
)
(
)
0 0 0
y f x x x f x
′
= − +
Enfin, on définit sans peine des dérivées d’ordre supérieur, et on rappelle les formules usuelles du
calcul des dérivées :
( )
( )
( )
( )
( ) ( ) ( )
( )
( )
2
1
0
n n
u v u v
uv u v uv
u u
u u v uv
v v
n x nx
uov x u v x v x
λ λ
λ λ
−
′′ ′
+ = +
′′ ′
= +
′
∈⇒=
′′
=
′′ ′
−
  =
′
∈⇒=
′
′ ′
=
ℝ
ℕ
§1 Les fonctions usuelles de l’analyse
a) Les fonctions trigonométriques. On rappelle ici les fonctions sinus, cosinus et tangente, leurs
graphes, le cercle trigonométrique, et quelques formules et valeurs à connaître pour les lignes
trigonométriques de
3 2
2 , , , , , , ,
6 3 4 2 2 3
π π π π π π
π π . Ces fonctions sont périodiques, le sinus et la
tangente sont des fonctions impaires, tandis que le cosinus est impair.

Il est important de savoir dessiner sans trop réfléchir, et sans recours à la calculette graphique, les
graphes des fonctions trigonométriques, leurs tangentes, leurs extremums, leurs points d’inflexion.
On peut remarquer sur ces exemples qu’il y a concomitance entre les faits suivants :
Lorsque la courbe est au-dessus de toutes ses tangentes, la dérivée seconde est positive ou
nulle, et réciproquement.
Ainsi, la dérivée seconde d’une fonction indique la convexité ou la concavité d’un graphe. Par voie
de conséquence, un point d’inflexion, qui n’est autre qu’un point où la courbe traverse sa tangente,
est aussi un point où la dérivée seconde s’annule en changeant de signe…
Ces phénomènes sont vrais pour toutes les fonctions qui ont au moins deux dérivées successives, et
l’on peut vérifier aussi qu’une dérivée seconde positive implique que l’arc de courbe est au-dessous
de la corde qui le sous-tend.
b) La fonction logarithme népérien . La fonction ln est définie sur
*
+
ℝ
, et sa propriété
fondamentale, qui la définit, se résume à :
Pour tout réel
0
x
>
,
( ) ( ) ( )
1
ln et ln 1 0
x
x
′
= =
On en déduit évidemment que la fonction ln est croissante, que son graphe est concave, on le
dessine avec ses propriétés en 0 et à l’infini.
On remarque, si l’on prend des valeurs de la fonction ln, ou s’il l’on fait dessiner le graphe par une
machine, son extrême mollesse à l’infini. Cela s’exprime en observant que la fonction
ln
x
x
α
tend
vers 0 en
+∞
, et ce pour tout réel
0
α
>
. Il faut noter toutefois que le graphe de la fonction
logarithme admet une asymptote verticale d’équation
0
x
=
, mais pas de maximum, pas
d’asymptote horizontale puisqu’elle tend vers
+∞
avec x . Il existe un unique réel e vérifiant
ln 1
e
=
, l’existence résulte du fait que la fonction ln varie de
−∞
à
+∞
et l’unicité résulte de la
stricte monotonie. On sait que
2,7182818
e
≈
⋯
. Attention, la suite des décimales n’est pas
périodique !
Enfin, on déduit des propriétés définissant ln la célèbre propriété algébrique :
Pour tous les réels a et b strictement positifs, on a
(
)
ln ln ln
ab a b
= +
c) La fonction exponentielle . La fonction exp est définie sur
ℝ
, et peut se déduire de la fonction
logarithme népérien comme sa fonction réciproque, plus précisément, le graphe suggère que pour
tout réel x, il existe un unique réel y avec ln
y x
=
. On pose alors exp( )
x y
=
, et on déduit de la
propriété
(
)
ln ln ln
ab a b
= + celle qui suit, tout aussi fondamentale :
(
)
(
)
(
)
exp exp exp
a b a b
+ =
On constate ici que la fonction exponentielle se comporte comme une extension à
ℝ
de la fonction
→
ℕ ℝ
définie par
n
n a
֏
pour un réel a donné, on a en effet
p q p q
a a a
+
=. Cette propriété est à
l’origine de la dénomination de la fonction exponentielle et de sa notation usuelle :

(
)
exp
x
x e
=
Et ceci n’est pas un hasard, on a bien
(
)
1
exp 1
e e
= =
Comme on le vérifiera aisément.
Le caractère de fonction réciproque de la fonction logarithme équivaut à la symétrie des graphes de
ces deux fonctions par rapport à la première bissectrice, dès lors qu’on dessine ces graphes dans un
repère orthonormal. On en déduit évidemment des propriétés corrélatives, comme la croissance, la
dérivée de la fonction exponentielle :
(
)
(
)
exp exp
x x
′=
la convexité, la raideur de cette fonction à l’infini, opposée à la mollesse du logarithme, qui
s’exprime en s’observant que la limite en
+∞
de
x
e
x
α
est
+∞
, quelle que soit la valeur du réel
positif
α
.
d) La fonction puissance . La fonction puissance
x x
α
֏
est définie sur
*
+
ℝ
pour tout réel
α
par la
relation
ln
x
x e
α α
=.
On a évidemment
x x x
α β α β
+
= et
( )
1
x x
α α
α
−
′=, si bien que cette fonction apparaît tout
naturellement comme un prolongement de la fonction banale
n
x x
֏
pour un entier n.
On déduit sans peine de cela que la fonction
x x
α
֏
est croissante si
0
α
>
, décroissante si
0
α
<
,
et l’on peut étudier en exercice sa convexité.
Enfin, on notera que pour 0
α β
< <
et 1
x
<
, on a
x x
α β
<
, et que si
1
x
<
, on a
x x
β α
<
, c’est
comme ça, et ça se vérifie aisément, et ça donne de jolis graphiques qu’on peut dessiner dans le
même repère.
§2 Approximation linéaire
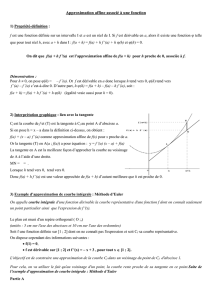
a) Qu’est-ce qu’une approximation linéaire ? Prenons une des fonctions étudiées ci-dessus, et
traçons, par exemple sur une machine graphique, le graphe de la fonction exponentielle au
voisinage de
0
x
=
. Sur le même écran, dessinons la tangente à ce graphe en ce point, dont
l’équation est
1
y x
= +
. Utilisant la fonction zoom de la machine, regardons à la loupe ce qui se
passe au voisinage du point
(
)
0,1
du graphe. Progressivement, l’écart entre la courbe et la droite
s’estompe, jusqu’à disparaître.
Cela signifie que la tangente en un point à un graphe est une bonne approximation de ce graphe (on
peut même démontrer que c’est la meilleure), et corrélativement, que la fonction tangente
(
)
1
t x x
= +
est une bonne approximation de
x
e
au voisinage de 0. Cette approximation est d’autant
meilleure que x est proche de 0. On pourra ainsi écrire les approximations linéaires classiques au
voisinage de 0 :

(
)
( )
ln 1
1
1 1
2
1 1
tan
sin
x
x x
e x
x
x
x x
x x
x x
α
α
+
+
+ +
+ +
≃
≃
≃
≃
≃
≃
qui sont couramment utilisées par les physiciens, particulièrement la dernière pour résoudre
l’équation du pendule.
b) Deux cas particulier simples à traiter
1. Concernant l’approximation 1 1
2
x
x
+ ≈ +
, on peut la démontrer facilement par le calcul, en
observant que
2
1 1 24 1 1
2
x x
x
x
x
−
+ − + =
  + + +
, ce qui indique par exemple que si 0
x
≤
, on a
2
1 1 0
8 2
x x
x
− 
≤ + − + ≤
, ou si l’on préfère (moi je préfère)
2
0 1 1
2 8
x x
x≤ + − + ≤ . Ce dernier
encadrement (que l’on peut compléter en considérant des x négatifs) dit à la fois la qualité de
l’approximation, par exemple que si
0 0,1
x
≤ ≤
, on a :
0 1 1 0,00125
2
xx≤ + − + ≤
et que le graphe de 1
x x
+
֏
est situé (à droite, mais on peut vérifier aussi cela à gauche) en
dessous de la tangente, ce qui est conforme aux indications de la dérivée seconde.
2. Approximation du sinus : On démontre que, pour tout x réel positif, on a l’encadrement
3 3 5
sin
6 6 120
x x x
x x x− ≤ ≤ − +
Il suffit pour cela d’étudier les fonctions f et g définies par
( )
3 5
6 120
x x
f x x= − + ,
( )
3
sin
6
x
g x x x
= − +
en les dérivant suffisamment. De cet encadrement, on peut déduire des
approximations de très bonne qualité de sinx pour des valeurs de x assez grandes, par exemple, on
voit que
5 5 1
sin1
6 6 120
≤ ≤ + , et un angle de un radian n’est pas un petit angle !
c) Approximation et calcul de l’erreur dans le cas général : Les calculs précédents améliorent
l’idée d’approximation linéaire, d’une part par le calcul de l’erreur, d’autre part dans le second cas,
par la recherche d’une amélioration de ladite erreur en prenant, non plus une approximation linéaire,
mais une approximation polynomiale. Le principe est qu’en fonction que l’on ne sait pas calculer

(sinus, logarithme, racine) peut être approchée par une fonction linéaire ou polynôme calculable
avec les moyens les plus élémentaires et avec une erreur qu’on sait mesurer.
On peut rencontrer les trois situations suivantes, qui relèvent toutes du même principe :
1. On se contente d’approcher la fonction f en x par la valeur connue de f en a¸ supposé voisin.
Dans ce cas on peut appliquer l’inégalité des accroissements finis qui dit :
Soit :f I
→
ℝ
, on suppose que a
∈
ℝ
, et qu’il existe un réel K tel que pour tout réel t de I, on a
(
)
f t K
′
≤
. Alors, pour tout réel x de I , on a
(
)
(
)
f x f a K x a
− ≤ −
.
2. Dans le cas de l’approximation linéaire par la tangente, on dispose d’une inégalité de Taylor
qui permet d’affirmer :
Soit : f I
→
ℝ
, on suppose que a
∈
ℝ
, et qu’il existe un réel K tel que pour tout réel t de I , on a
(
)
f t K
′′
≤
. Alors, pour tout réel x de I , on a
( ) ( ) ( )( )
2
2
K x a
f x f a f a x a −
′
− − − ≤ . On peut
comparer ce résultat à ce qui a été calculé « à la main » pour 1
x
+
.
3. De façon plus générale, on peut utiliser une inégalité de Taylor à un ordre supérieur :
Soit : f I
→
ℝ
, on suppose que a
∈
ℝ
, et qu’il existe un réel K tel que pour tout réel t de I , on a
( )
( )
1 n
f t K
+
≤
pour un entier n donné. Alors, pour tout réel x de I , on a
( ) ( ) ( )( ) ( )( )
( )
( )( ) ( )
1
2
2! ! 1 !
n
n
n
K x a
f a x a f a x a
f x f a f a x a n n
+
′′ −− −
′
− − − − − − ≤ + ⋯ . On peut
comparer ce résultat à ce qui a été calculé « à la main » pour la fonction sinus avec
0, 4
a n
= =
.
L’intérêt, là encore, est de pousser le développement de Taylor de la fonction f aussi loin que
nécessaire pour que l’erreur
( )
1
1 !
n
K x a
n
+
−
+soit petite, ce qui dépend de K, mais aussi de n, car si le
nombre
x a
−
est sensiblement inférieur à 1, alors
( )
1
1 !
n
x a
n
+
−+ devient très vite très petit, pourvu que
la dérivée
(
)
1
n
f
+
reste « raisonnable »…
d) Un exercice, pour se rassurer : Soit à donner une approximation linéaire intelligente de
ln(2,7).
On observe d’abord que le nombre 2,7 est proche de e , on va donc proposer une approximation
linéaire à partir de e . L’équation de la tangente au graphe de ln en e est donnée par :
( )
1ln
x
y x e e
e e
= − + =