ANALYSE STATISTIQUE pour la gestion

Pr. Alain FRANCOIS-HEUDE [e-mail]
Université de MONTPELLIER IUT GEA 2éme année FI 2016-2017
du bon usage de la statistique en gestion…
MAD41F
ENT MOODLE Cours : AFH GEA2FI Cours 2016-2017
ANALYSE STATISTIQUE
pour la gestion
Cours N° 1 : Rappel sur les lois usuelles

2

3
Généralités
Objectif : Maîtriser quelques outils quantitatifs d’aide à la décision en gestion
Pédagogie : 6 heures de cours et 7 séances de 2h de TD par groupe
- Priorité à l’interprétation des outils et des méthodes
- Réalisation de cas avec discussion des résultats obtenus
- Utilisation du logiciel Excel comme support pédagogique
- Contrôles pour l’évaluation
a) – un contrôle (QCM) pendant un TD
b) – individuel avec document, en semaine bloquée
Espace pédagogique :
1 - accéder au site par https://ent.umontpellier.fr
ou par http://www.umontpellier.fr puis onglet « ENT » puis s’identifier
2 - sélectionner le site du cours :
‘AFH GEA2FI Cours 2016-2017’ Dossier ‘Statistiques Inférentielles’

4
La statistique inférentielle
===========================
- Introduction : Rappel sur les lois
- Estimation * directe d’un paramètre
* par intervalle de confiance
- Test d’hypothèses
* indépendance et ajustement
* sur les paramètres
- Conclusion
PLAN

5
Rappel sur quelques lois statistiques
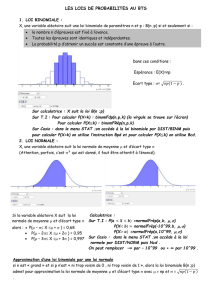
• La loi Binomiale B ( n , p )
• La loi de Poisson P ( λ)
• La loi de Student Stv( μ, σ)
Avant d’évoquer la loi du Khi Deux et celle de Fisher …
•La loi Normale N ( μ, σ)