1 247,208: Partie entière , Partie décimale Partie entière , Partie

Nombres entiers – nombres décimaux Page 1
Nombres entiers – Nombres décimaux
1. Ecriture d’un nombre :
3 747 ; 238 ; 10 004 sont des nombres entiers
27,3 ; 0,007 5 ; 1 247,208 sont des nombres décimaux
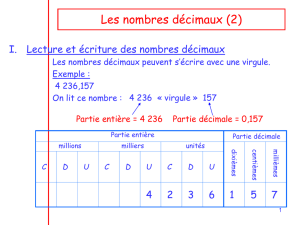
Dans le nombre 1 247,208 :
1 247 est la partie entière
208 est la partie décimale
La virgule sépare partie entière et partie décimale du nombre
Un nombre décimal s’écrit donc sous la forme :
Partie entière , Partie décimale
2. Noms des chiffres constituant un nombre décimal :
Partie entière
,
Partie décimale
millions
milliers
Unités simples
Centaines de million
Dizaines de millions
Unités de millions
Centaines de mille
Dizaines de mille
Unités de mille
centaines
dizaines
unités
Dixièmes
Centièmes
Millièmes
Dixmillièmes
Centmillièmes
millionièmes
Dans le nombre 9 347 , 215
1 est le chiffre des centièmes
3 est le chiffre des centaines
Le chiffre des unités est 7
Le chiffre des unités de mille est 9
Le chiffre des millièmes est 5
Ce nombre se lit :
« neuf mille trois cent quarante-sept unités et deux cent quinze millièmes » ( on
utilise partie entière et partie décimale pour lire le nombre)
Ou
« neuf millions trois cent quarante-sept mille deux cent quinze millièmes » ( on lit le
nombre en fonction du rang du dernier chiffre écrit)

Nombres entiers – nombres décimaux Page 2
3. Ecriture fractionnaire décimale d’un nombre :
Vingt-cinq dixièmes s’écrit 2,5 ou
10
25
Deux cent cinquante centièmes s’écrit 2,5 ou
100
250
Deux mille cinq cents millièmes s’écrit 2,5 ou
1000
2500
Un nombre décimal peut s’écrire à l’aide d’une fraction dont le dénominateur est 10,
100, 1 000, …Cette fraction est une « fraction décimale ».
Un nombre décimal peut s’écrire de plusieurs façons différentes sous la forme d’une
fraction décimale.
4. Comparaison de deux nombres décimaux :
a/ Règle de comparaison :
De deux nombres décimaux, le plus grand est celui qui a la partie entière la plus
grande.
Si les deux nombres décimaux ont la même partie entière, on compare les deux
parties décimales en commençant par les dixièmes, puis en cas d’égalité en
comparant les centièmes, puis les millièmes, …
Exemples : 37,4 > 32,8 ; 24,328 < 24,41
b/ Rappels :
« < » se lit « plus petit que … » ou « inférieur à … »
« > » se lit « plus grand que … » ou « supérieur à … »
c/ Remarques :
On peut ranger une série de nombres :
 Dans l’ordre croissant : du plus petit au plus grand
 Dans l’ordre décroissant : du plus grand au plus petit
Dans la liste : 2 ; 2,02 ; 22,2 ; 22,02 ; 20,02 ; 0,22
Dans l’ordre croissant : 0,22 < 2 < 2,02 < 20,02 < 22,02 < 22,2
Dans l’ordre décroissant : 22,2 > 22,02 > 20,02 > 2,02 > 2 > 0,22
5. Encadrement d’une valeur :
Encadrer une valeur, c’est la situer entre une valeur plus petite et une valeur plus
grande.
Exemples : 1,7 < 3,8 < 4,5
Un rectangle a une longueur en cm nommée L telle que : 3,2 < L < 7,8
Encadrer une valeur à l’unité près, c’est la situer entre les deux entiers les plus
proches.
Exemples : 3 < 3,8 < 4
1 < 1,475 < 2

Nombres entiers – nombres décimaux Page 3
Encadrer une valeur au dixième près, c’est la situer entre les deux valeurs décimales
n’ayant qu’un chiffre après la virgule les plus proches.
Exemples : 3,2 < 3,27 < 3,3
5,3 < 5,328 < 5,4