Trigonométrie 2 TCS Résumé

Prof/ATMANI NAJIB http:// www.xriadiat.com 1
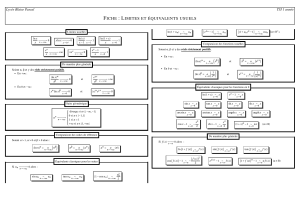
I) Les équations trigonométriques élémentaires
1) Equation:
cos xa
Soit
a
un nombre réel.
Si
1a
ou
1a
alors l’équation
cos xa
n’admet pas de solution dans et on a :
S
.
Si
11a  
alors il existe un unique réel : dans
0;
tel que
cos cosx
et alors on a :
2 ; 2 /S k k k
.
2) Equation:
sinxa
Si
1a
ou
1a
alors l’équation
sinxa
n’admet pas de solution dans et on a :
S
.
Si
11a  
alors il existe un unique réel : dans
;
22
tel que
sin sinx
et alors on a :
2 ; 2 /S k k k
.
3) Equation :
tan xa
L’équation
tan xa
est définie dans équivaut à :
2
xk
avec k un nombre relatif
Il existe un unique réel : dans
;
22
tel que
tan tanx
et alors on a :
/S k k
.
Des équations trigonométriques élémentaires :
Équivaut à :
k
Équivaut à :
k
Équivaut à :
k
Équivaut à :
k
Équivaut à :
k
Équivaut à :
k
II) Les inéquations trigonométriques élémentaires - Méthode :
Comme pour les équations, on cherche à se ramener à une inéquation du type sin(α)⩽sin(β)
ou cos(α)⩽cos(β) ou tan(α)⩽tan(β), en remplaçant au besoin ⩽ par ⩾ , < ou >.
Le cercle trigonométrique permet de mieux visualiser les intervalles solutions.
Remarque : Pour les inéquations trigonométriques il est pratiquement impossible de résoudre sans
dessiner un cercle trigonométrique
cos 1x
2xk
cos 0x
2
xk
cos 1x
21xk
sin 1x
2
2
xk
sin 0x
xk
sin 1x
2
2
xk
TRIGONOMÉTRIE2 Tronc commun Sciences BIOF
Partie 2 : Equations et inéquations trigonométriques
Résumé de Cours
Mostafa QASSOUOUI