Oscillateur

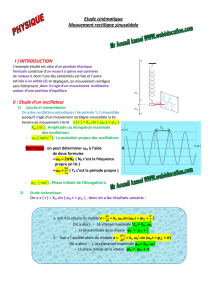
x(t)
x(t) = xmcos(ω0t+φ)
x(t)
xm
ω0
ω0t+φ
φ
T0=2π
ω0T0
¨x+ω0x= 0
k=m.ω2
0
Ep(x) = E(x0= 0) + 1
2
d2Ep
dx2|x0=0x2
Ep(x) = E(0) + 1
2k.x2=E(0) + 1 2kx2
mcos2(ω0t+φ)
Ec=1
2mv2=1 2m˙x
Ec=1
2mω2
0sin2(ω0t+φ)
Em=Ec+Ep=Ep(0) + 1
2kx2
m=cte
EcEp
Ep(0) = 0
< Ec>=1
T0
T0
0
Ecdt =1
4kx2
m
< Ep>=1
T0
T0
0
Epdt =1
4kx2
m
< Em>=1
2kx2
m
< Ec>=< Ep>=< Em>
2

¨x+ω0
Q˙x+ω2
0x=ω2 0d
ω0
Q
2α=ω0
Q
dEm
dt =p(⃗
Fnc) = −λv2<0
λ
X=x−d
¨x+ 2α˙x+ω2
0x= 0
∆=4α2−4ω2
0
∆>0⇒α > ω0⇒Q < 1
2
r±=−α±qα2−ω2
0
x(t) = Aexp(r+t) + Bexp(r−t)
x(t) = exp(−αt)(Aexp(qα2−ω2
0.t) + Bexp(−qα2−ω2 0.t))
1 2 3 4 5
−2
2
t
∆=0 ⇒α=ω0⇒Q=1
2
r=−α
x(t)=(At +B) exp(−αt)
x(t) = exp(−αt)(At +B)

1 2 3 4 5
−2
2
t
∆<0⇒α < ω0⇒Q > 1
2
r±=−α±iqω2
0−α2
x(t) = exp(−αt)(Aexp(iqω2
0−α2t) + Bexp(−iqω2 0−α2t))
x(t) = exp(−αt)(A′cos(qω2
0−α2.t +φ))
x(t) = exp(−αt)(A′cos(Ω.t +φ))
Ω
12345
−2
2
t
T=2π
Ω=T0
q1−(α
ω0)2
=T0
q1−1
4Q2
δ=α.T
x(t) = Aexp(−αt) cos(Ωt+φ)
x(t+nT ) = Aexp(−α(t+nT )) cos(Ωt+φ) = x(t) exp(−αnT )
αnT = ln( x(t)
x(t+nT ))

n= 1
δ=αT = ln( x(t)
x(t+T))
δ=2π
p4Q2−1
δ Q
α→0⇒Q≫1⇒ω0≫α
Ω = ω0r1−1
4Q2≃ω0
x(t) = Aexp(−αt)(cos(ω0t+φ))
Ep=1
2k.x2=1 2k.A2exp(−2αt) cos2(ω0+φ)
Ec=1
2m. ˙x2=1 2m.A2exp(−2αt)(−αcos(ω0+φ)−ω0sin(ω0t+φ))2
Ec≃1
2m.A2ω2
0exp(−2αt) sin(ω0t+φ)
Em=k.A2
2exp(−2αt)
Em(t)−Em(t+T)
Em(t)
Q= 2πEnergie d′oscillateur
Energie perdue pendant une pseudo −periode
e= 2,718
τ= 1/α Q ≫1
Q=ω0τ
2
x
⃗
P+⃗ R+⃗ f+⃗ T+⃗ F(t) = m⃗a
Ox
−kx −λ˙x+F(t) = m¨x
¨x+ 2α˙x+ω2
0x=F(t)
m

x(t)
x(t) = xh+xp
xh∆
xp=Xcos(ωt +φp)F(t) = F0cos(ωt +φ)
xh
xp
x(t) = Xcos(ωt +φ))
x(t) = Xcos(ωt +φ)−→ x(t) = Xexp(i(ωt +φ)) = Xexp(iωt)
X=Xexp iφ
X=|X|φ= arg(X)
F(t) = F0cos(ωt)−→ F(t) = F0exp(iωt)
¨x(t) + 2α˙x(t) + ω2
0x(t) = F0
mexp(iωt)
˙x(t) = iωx(t) ¨x(t) = −ω2x(t)
x(t)(−ω2+ 2iαω +ω2
0) = F0
mexp iωt
X=F0/m
ω2
0−ω2+ 2iαω
X=F0/m
ω2
0−ω2+iω0ω
Q
X=|X|=F0/m
q(ω2
0−ω2)2+ (ω0ω
Q)2
0.5 1 1.522.5 3
1
2
3
4
5
Xmω2
0
F0
ω
ω0
ω→0⇒X=F0/(mω2
0)
ω→ ∞ ⇒ X→0
dX
dω = 0 ⇒ωr=ω0r1−1 2Q2⇒Q > 1
√2≃0.7
Q≫1⇒ωr→ω0
Q > 1/√2
Q < 1/√2