TP-MDF-vidange-1

1
But de travail :
Le but de ce travail est dans un premier temps, d’étudier le mode d’écoulement d’un
liquide par un orifice latéral d’un réservoir, de grande dimensions par rapport à celles de
l’orifice. Dans un second temps, les résultats expérimentaux seront confronté à ceux prédits
par la théorie.
1ére partie :
Vidange par un orifice latéral :
Mode opératoire :
1) Relevez les caractéristiques géométriques du réservoir ( le diamètre du réservoir D1
et le diamètre de l’orifice D2 ), puis remplissez ce dernier tout on maintient l’orifice fermer ,
relevez le niveau initiale h0, après cela ouvrir l’orifice et déclenchez le chronomètre au même
temps, puis dans chaque 5 seconds relevez le niveau de l’eau (h) correspondent jusqu’à
atteindre le vidange totale du réservoir. Porter les résultats obtenus sur un tableau.
2) Donc on obtient le tableau des résultats suivant :
t(s)
0
5
10
15
20
25
30
35
40
45
50
55
60
65
H(cm)
51.5
49.1
46.3
41.8
39.5
37.2
35.4
33.2
31.4
29.2
27.2
25.6
23.7
21.8
t(s)
70
75
80
85
90
95
100
105
110
115
120
125
130
135
h(cm)
20.6
18.9
17.6
16
14.9
13.4
12
10.9
9.7
8.8
7.8
6.8
5.9
4.8
140
145
150
155
160
165
170
175
180
185
190
4.1
3.6
3
2.6
2.3
1.5
1.3
1
0.7
0.5
0.3
3) Établissons l’équation différentielle qui régit β(t) :
z
(1)
z V1 ,A1
g
h
V2,A2
(2)
z0

2
Appliquant l’équation de Bernoulli instationnaire entre les points (1) et (2) :
AgzPdl
dt
Vd
II
I
V................0
2
12
1
2
2
1
on a :(I) =
2
1
dl
dt
Vd
=
2
1
1dz
dt
dV
=
2
1
1z
dt
dV
=
dt
dV1
[z0 - z ]
or : z0 = 0 et z = h
Donc :
(I) =
h
dt
dV1
et on a : (II) =
VV ghPagPa 2
1
2
22
1
2
1
0
=
gh
V
V
V
2
2
2
1
2
21
2
1
puisque le fluide est parfait donc : ρ = cte
 Q = A1 V1 = A2 V2 
V
V
A
A
2
1
1
2
On a A2 < A1 
A
A
1
2
< 1, donc
V
V
2
1
< 1
(II) =
gh
V
2
2
2
1
donc : (A) 
h
dt
dV1
+
gh
V
2
2
2
1
= 0
dt
d
hV1
+
gh
V
2
2
2
1
= 0………………………….(1)
on a A1 V1 = A2 V2 
V
A
A
V2
1
2
1
………………………………..(2)
et posons
h
V
g0
2
2
hV g02 2
…………………(3)

3
Substituons (2) et (3) dans (1) on obtiens :
0*
2
0
2
0
1
0
2 hh
Ah
Ah
dt
d
g
gh
(c’est l’équation différentielle qui régit β(t) )
2
0
0
2
00
1
0
21*
2h
hh
dt
d
g
gh h
hhh
Ah
A
2
0
1
0
21*
2hdt
d
g
gh
Ah
A
dt
g
g
h
dh
AA
h0
2
1
2
02
1
dt
g
g
h
dh
AA
h0
2
1
2
02
1
Posons
2
0
2
h
h
h
h0
h
d
dh0
h
h
dd
0
Donc :
dt
g
g
d
hh
AA
h0
2
1
2
02
1
*
dt
gh
g
dAA
2
12
1
2
tdt
gh
g
dAA
0
2
1
022
1
t
gh
g
AA
2
1
1
log
2
1
2
1
h
t
g
K
A
A*
2
1
1
log
2
1

4
eh
t
k
1 1
donc
on a
h
h0
donc
et on a
hV g02 2
don c
- Détermination de la valeur de V(sortie) (c’à’d V2) quand t tend vers l’infinie :
On a quand t   
e
e
h
t
k
h
t
k
1
1
 1
Donc
4) comparaison des valeurs avec celles prédit par la théorie :
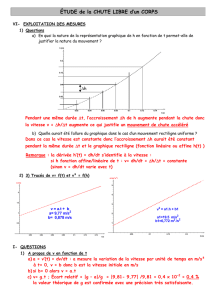
la hauteur en fonction du temps
0.000
1.000
2.000
3.000
4.000
5.000
6.000
7.000
8.000
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 135
e
e
h
t
k
h
t
k
1
1
e
e
hh
t
k
h
t
k
h
1
1
*
0
e
e
Vh
t
k
h
t
k
gh  1
1
*2
2
gh
V2
2

5
On remarque que
h
varie linéairement avec le temps, et d’après la
relation
gh
V2
2
c’est une équation d’une droite donc les résultats confronte à ceux
prédit par la théorie.
Alors la vitesse d’éjection varie linéairement en fonction du temps donc
c’est un écoulement quasi-stationnaire.
5) détermination du temps de vidange :
on a :
Q = A1V1 = A2V2 
gh
dt
dh AA 2
21 
dt
gh
dh A
A
1
2
2
0
2
1
00
2hh
dh
g
dt AA
T
g
h
h
g
Th
A
A
AA2
20
2
1
0
2
122 0
AN:
A1 et A2 = ??
P1 = 110 cm = D1  D1 = 110/ donc D1 = 35.014 cm 
D2 = 14.95 mm 
h0 = 48.5 * 10-2 m
donc
81.9 *5.48*2
*754.1
*628.9 10
10
10 2
4
2
T
On remarque que le temps de vidange théorique est inférieur à celui déterminer
pratiquement et cela est du à l’existence des frottements.
g
Th
A
A20
2
1
A1 = 9.628 * 10-2 m2
A2 = 1.754 * 10-4 m2
T = 172.64 s