Sequence 0 - Automatismes

Chapitre E
Automatismes : 1ere STD2A
Sommaire
I) Fonctions et représentations .................................. 2
1) Déterminer graphiquement des images et des antécédents . . . . . . . . . . . . . . . . . . . 2
2) Résoudre graphiquement une équation, une inéquation du type : f(x) = k,f(x)> k ... . . . 3
II) Solutions des exercices ..................................... 5
S. BALNY 11ere STD2A

Fonctions et représentations Automatismes : 1ere STD2A
I) Fonctions et représentations
1) Déterminer graphiquement des images et des antécédents
Une fonction est un procédé qui à un nombre xappartenant à un ensemble Dassocie un nombre y.
On note : xf 7→ you encore f:x7→ you encore y=f(x).
On dit que yest l’image de xpar la fonction fet que xest un antécédent de ypar la fonction f.
Fonction, Image, Antécédents :
Soit gla fonction définie par g(x) = x2+ 3.
•L’image de 5est g(5) = 52+ 3 = 28,
•Les antécédents de 7vérifient g(x) = 7 c’est à dire x2+ 3 = 7 soit x=−2ou x= 2,
•Il n’y a pas d’antécédent de 1car l’équation g(x) = 1 n’a pas de solution : x2+ 3 = 1 ⇐⇒ x2=−2.
Exemple :
Soit hla fonction définie par la courbe bleue suivante :
0123456−1−2−3
0
−1
−2
−3
1
2
3
4
y=−2
03
x= 5
•L’image de 5par hest 3.
•Les antécédents de −2par hsont 0et 3.
Exemple :
S. BALNY 21ere STD2A

Fonctions et représentations Automatismes : 1ere STD2A
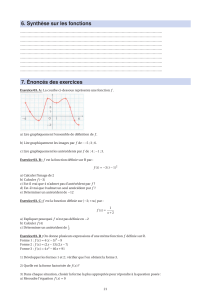
Exercice E1 On considère la fonction f. En voici une représentation graphique :
0 1 2 3 4 5 6 7 8 9 10−1−2
0
−1
−2
1
2
3
Cf
1. Déterminer les images par fde −2,1,4,5,6.
2. Déterminer les antécédents éventuels de −2,−1,0,2et 3par f
2) Résoudre graphiquement une équation, une inéquation du type : f(x) = k,f(x)> k ...
Soit fla fonction définie par la courbe bleue suivante :
012345−1
0
−1
−2
−3
1
2
3
•L’équation f(x) = 0 admet deux solutions : 0et 4.
•L’équation f(x)¾1,5admet pour ensemble solution [1; 3] car, graphiquement, l’inéquation correspond
à la partie verte de la courbe :
01234−1
0
−1
−2
−3
1
2
1 2
1,5
Exemple :
S. BALNY 31ere STD2A

Fonctions et représentations Automatismes : 1ere STD2A
Exercice E2 Sur [−2,5; 3,5], on considère la fonction gsuivante :
0 1 2 3−1−2
0
−1
−2
−3
1
2
3
4
1. Résoudre l’équation f(x) = 0.
2. Résoudre l’équation f(x) = −1.
3. Résoudre l’équation f(x) = −3.
4. Résoudre l’inéquation f(x)¶−2.
5. Résoudre l’inéquation f(x)>1.
S. BALNY 41ere STD2A

Solutions des exercices Automatismes : 1ere STD2A
II) Solutions des exercices
Correction E1
1. L’image de −2 par fest 0. On écrit f(−2) = 0.
De même, on a f(1) = 1 ; f(4) = 3 ; f(5) = 2 et f(6) = 0.
2. −2 n’a pas d’antécédent par f.
6,5 et 8 sont les antécédents de −1 par f.
Les antécédents de 0 par fsont −2 ; 6 et environ 8,7.
Les antécédents de 2 par fsont 3 et 5. L’antécédent de 3 par fest 4.
Correction E2
Attention, la lecture graphique n’est pas exacte. Il s’agit d’être le plus précis possible mais l’exactitude est impos-
sible.
1. L’équation f(x) = 0 admet pour solutions −2 ; −1 ; 1 et 3.
2. L’équation f(x) = −1 admet pour solutions 1,4 et 2,8.
3. L’équation f(x) = −3 n’admet pas de solution.
4. L’inéquation f(x)¶−2 admet pour ensemble solution [1,8; 2,6].
5. L’inéquation f(x)>1 admet pour ensemble solution [−2,5; −2,2[∪]−0,3; 0,4[∪]3,1; 3,5].
S. BALNY 51ere STD2A