6 symetrie axiale exercices

6 symetrie axiale exercices Page 1 sur 7
E XERCICE 1 Construire les médiatrices des segments suivants en utilisant la règle graduée et l’équerre :
Coder les figures obtenues
Conseil prendre l’habitude de tracer la médiatrice « plus longue » que le segment, car c’est une droite
E XERCICE 2 On a tracé un segment [AB] ainsi que sa médiatrice (d).
Les points M
1
, M
2
, M
3
et M
4
appartiennent à (d).
Les points P
1
, P
2
, P
3
et P
4
n’appartiennent pas à (d).
a. Mesurer à la règle (et au mm près) les longueurs suivantes :
M
1
A = …… M
1
B = …… M
2
A = …… M
2
B = ……
P
1
A = …… P
1
B = …… P
2
A = …… P
2
B = ……
M
3
A = …… M
3
B = …… M
4
A = …… M
4
B = ……
P
3
A = …… P
3
B = …… P
4
A = …… P
4
B = ……
b. Que remarque-t-on ?
E XERCICE 3
Construire les médiatrices des segments suivants en utilisant le compas :
Conseil penser à coder ! et tracer la médiatrice « plus longue » que le segment, car c’est une droite
E XERCICE 4 Construire les médiatrices des segments suivants en utilisant le quadrillage :
4 cm
2 cm
5 cm
4,3 cm
A
B
C
D
E
F
G
A
B
C
D
E
F
H
G
I
J
K
L
M
N
O
P
H
A
B
M
2
(d)
P
1
P
2
P
4
P
3
M
1
M
3
M
4

6 symetrie axiale exercices Page 2 sur 7
E XERCICE 5 Pour chaque figure, lequel des points M
1
, M
2
ou M
3
semble être le symétrique de M par rapport à
(d) ?
 M
1
 M
2
 M
3
 M
1
 M
2
 M
3
 M
1
 M
2
 M
3
E XERCICE 6
« B est le symétrique de A par rapport à une droite (d) revient à dire que (d) est la médiatrice de [AB] »
Compléter les phrases suivantes :
a. F est le symétrique de E par rapport à une droite (d) revient à dire que ...... est la médiatrice de ........ .
b. R est le symétrique de M par rapport à une droite (xy) revient à dire que ...... est la médiatrice de ........ .
e. .... est le symétrique de J par rapport à une droite ...... revient à dire que (d) est la médiatrice de [IJ] .
f. .... est le symétrique de D par rapport à une droite ...... revient à dire que (xy) est la médiatrice de [CD] .
E XERCICE 7
a/ Construire les symétriques de A, B, C et D par
rapport à (d) en utilisant l’équerre :
b/ Construire les symétriques de E, F, G et H par
rapport à (∆) en utilisant le compas :
M
M
M
M
1
M
1
M
1
M
2
M
2
M
2
M
3
M
3
M
3
(d)
(d)
(d)
(d)
A
B
C
D
E
F
G
H
(
∆
)

6 symetrie axiale exercices Page 3 sur 7
E XERCICE 8
a. Construire le point A’ tel que (d) soit la médiatrice de [AA’] en utilisant la règle graduée (ou le compas).
b. Construire de la même manière les points B’ et C’ tel que (d) soit la médiatrice de [BB’] et [CC’].
c. Construire le point D’ tel que (d) soit la médiatrice de [DD’] en utilisant l’équerre et la règle graduée.
d. Construire de la même manière les points E’, F’ et G’ tel que (d) soit la médiatrice de [EE’], [FF’] et [GG’].
Plier la feuille suivant la droite (d). Que remarque-t-on ?
Exercice 9
A
B
C
D
F
E
G
(d)

6 symetrie axiale exercices Page 4 sur 7
Exercice 10
Construire dans chaque cadre le symétrique de la droite (d) par rapport à l’axe (∆) :
Exercice 11
Exercice 11 B
Entourer le nom des segment qui correspondent
(D1) est la
médiatrice
de
(D2) est la
médiatrice
de
(D3) est la
médiatrice
de
(D4) est la
médiatrice
de
[AH]
[AI]
[AD]
[CD]
[EF]
[EH]
[EG]
[GF]
[DF]
[DI]
[HF]
[AH]
[AI]
[AD]
[CD]
[EF]
[EH]
[EG]
[GF]
[DF]
[DI]
[HF]
[AH]
[AI]
[AD]
[CD]
[EF]
[EH]
[EG]
[GF]
[DF]
[DI]
[HF]
[AH]
[AI]
[AD]
[CD]
[EF]
[EH]
[EG]
[GF]
[DF]
[DI]
[HF]
a.
b.
(
∆
)
(
∆
)
(d)
(d)

6 symetrie axiale exercices Page 5 sur 7
Exercice 12 Construire dans chaque cadre le symétrique de la figure (demi-droite, segment ou cercle) par rapport à (∆) :
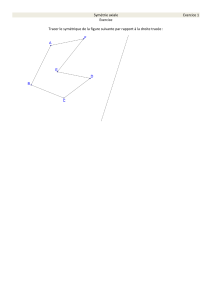
Exercice 13 Construire les symétriques des figures suivantes par rapport à l’axe (∆)
a
.segment[AB]
b.
demi-droite [Ox)
c.
d.
segment[AB]
(
∆
)
(
∆
)
(
∆
)
(
∆
)
A
B
O
x
A
B
A
B
C
D
O
E
F
G
H
I
J
K
L