2- Chap2-f(x)=0(1)

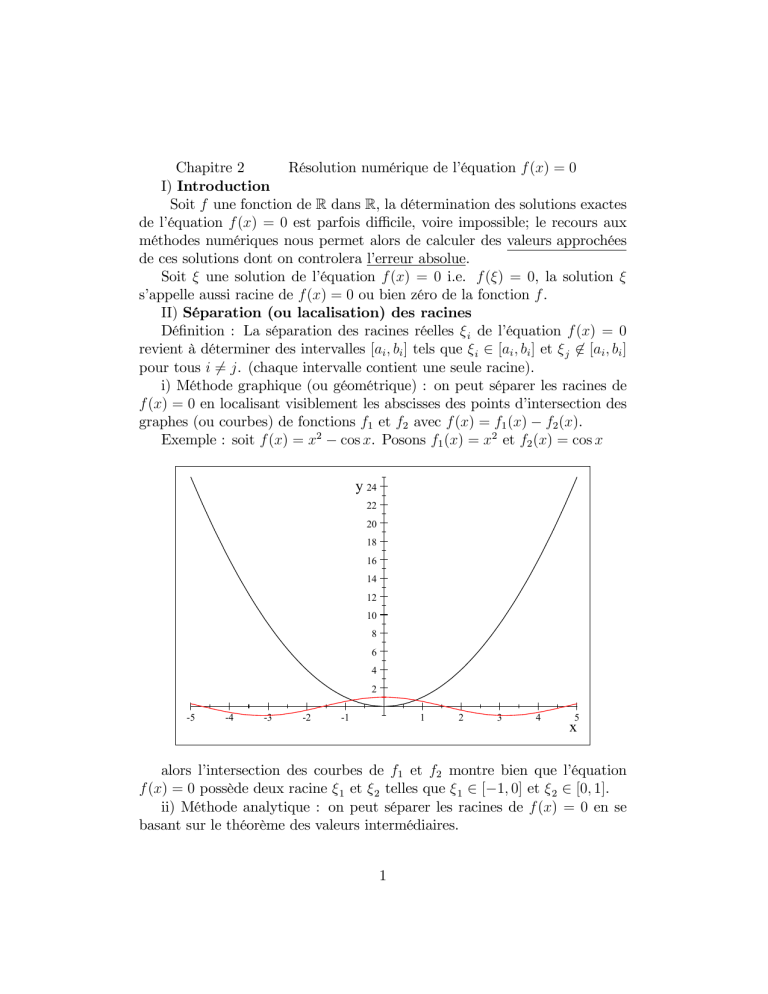
Chapitre 2
Résolution numérique de l’équation f (x) = 0
I) Introduction
Soit f une fonction de R dans R, la détermination des solutions exactes
de l’équation f (x) = 0 est parfois di¢ cile, voire impossible; le recours aux
méthodes numériques nous permet alors de calculer des valeurs approchées
de ces solutions dont on controlera l’erreur absolue.
Soit une solution de l’équation f (x) = 0 i.e. f ( ) = 0, la solution
s’appelle aussi racine de f (x) = 0 ou bien zéro de la fonction f .
II) Séparation (ou lacalisation) des racines
Dé…nition : La séparation des racines réelles i de l’équation f (x) = 0
revient à déterminer des intervalles [ai ; bi ] tels que i 2 [ai ; bi ] et j 62 [ai ; bi ]
pour tous i 6= j. (chaque intervalle contient une seule racine).
i) Méthode graphique (ou géométrique) : on peut séparer les racines de
f (x) = 0 en localisant visiblement les abscisses des points d’intersection des
graphes (ou courbes) de fonctions f1 et f2 avec f (x) = f1 (x) f2 (x).
Exemple : soit f (x) = x2 cos x. Posons f1 (x) = x2 et f2 (x) = cos x
y 24
22
20
18
16
14
12
10
8
6
4
2
-5
-4
-3
-2
-1
1
2
3
4
5
x
alors l’intersection des courbes de f1 et f2 montre bien que l’équation
f (x) = 0 possède deux racine 1 et 2 telles que 1 2 [ 1; 0] et 2 2 [0; 1].
ii) Méthode analytique : on peut séparer les racines de f (x) = 0 en se
basant sur le théorème des valeurs intermédiaires.
1
Théorème : Soit f : [a; b] ! R une fonction continue, si f (a)f (b)
0
alors il existe 2 [a; b] tel que f ( ) = 0 (…n du théorème).
Si de plus f est strictement monotone sur [a; b] alors est unique.
Exemple : soit f (x) = 2x e x . On a lim f (x) = 1, lim f (x) =
x! 1
x!+1
+1 et f 0 (x) = 1 + e x > 0 sur R alors l’équation f (x) = 0 possède une
unique racine réelle . De plus, on a f (0) = 1 < 0 et f (1) = 2 e 1 > 0
donc 2 [0; 1].
Dé…nition : Etant donné une solution d’une équation f (x) = 0, si (xn )
est une suite obtenue par un algorithme censé approcher , on dira que cet
algorithme converge si lim xn = , dans ce cas les termes x0 ; x1 ; :::; xn ; :::
n!+1
sont des valeurs approchées de .
On appelle erreur d’approximation (d’ordre n) de l’algorithme la quantité
j.
n = jxn
III) Méthode de Dichotomie (ou de la bissection) : c’est un algorithme basé sur le théorème des valeurs intermédiaires qui consiste à répéter
des partages d’un intervalle en deux parties puis à sélectionner le sousintervalle dans lequel existe un zéro de la fonction.
Soit f : [a; b] ! R une fonction. On suppose que
i) f est continue sur [a; b]
ii) f (a) f (b) < 0
iii) il existe un unique 2 [a; b] tel que f ( ) = 0
Alors, on dé…nit trois suites (an ), (bn ) et (xn ) de la manière suivante :
a0 + b 0
a0 = a; b0 = b et x0 =
2
Si f (x0 )f (b0 ) 0 alors 2 [x0 ; b0 ], prendre a1 = x0 et b1 = b0 :
Si f (x0 )f (b0 ) > 0 alors 2 [a0 ; x0 ], prendre a1 = a0 et b1 = x0 :
a1 + b 1
Prendre x1 =
2
Si f (x1 )f (b1 ) 0 alors 2 [x1 ; b1 ], prendre a2 = x1 et b2 = b1 :
Si f (x1 )f (b1 ) > 0 alors 2 [a1 ; x1 ], prendre a2 = a1 et b2 = x1 :
a2 + b 2
Prendre x2 =
2
Ainsi de suite on construit des intervalles [a1 ; b1 ]; [a2 ; b2 ]; :::; [an ; bn ] et une
an + b n
suite xn =
tels que 2 [an ; bn ] ::: [a2 ; b2 ] [a1 ; b1 ] [a0 ; b0 ].
2
Théorème : Avec les mêmes notations, on a
1
i) 0 < bn an = n (b0 a0 ).
2
ii) Les suites (an ), (bn ) et (xn ) convergent vers .
2
jb0 a0 j
iii) L’erreur d’approximation véri…e n = j
xn j
; 8n 0.
2n+1
Preuve
1
i) il est clair que bn an = n (b0 a0 ) ! 0 quand n ! +1
2
ii) Noter que (an ) est croissante et que (bn ) est décroissante donc (an ) et
(bn ) sont adjacentes, alors elles convergent vers la même limite l 2 R. Comme
an + b n
xn =
donc (xn ) converge aussi vers l. Mais an
bn donc
2
quand n ! +1 on obtient l
l d’où = l:
an b n
iii) On a an
bn donc an xn
xn bn xn d’où
2
b n an
jbn an j
jb0 a0 j
xn
alors j
xn j
=
.
2
2
2n+1
IV) Méthode du Point …xe (ou des approximations successives)
Dé…nitions : Soit ' : R ! R une fonction.
i) On dit qu’un réel est un point …xe de ' si '( ) = .
ii) On dit que ' est stable sur le segment [a; b] si '([a; b]) [a; b].
iii) On dit que ' est lipschitzienne sur [a; b] s’il existe une constante
k 2 R+ tel que j'(x) '(y)j
k jx yj pour tout (x; y) 2 [a; b]2 . Si de
plus k 2 [0; 1[, on dira que ' est contranctante sur [a; b].
Théorème du point …xe : Soit ' : R ! R une fonction. Si ' est stable
et contractante sur [a; b] de constante k, alors la suite récurrente (xn ) dé…nie
par xn+1 = '(xn ) converge vers l’unique point …xe de ' sur [a; b] et ceci
pour tout x0 de [a; b]. L’erreur d’approximation véri…e n = jxn
j
kn
jx1 x0 j, 8n 1.
1 k
Preuve :
i) Montrons que ' admet un unique point …xe : comme ' est contractante
sur [a; b] donc elle est continue sur [a; b]. Soit (x) = '(x) x, alors (a) =
'(a) a 0 et (b) = '(b) b 0 donc il exsite 2 [a; b] tel que ( ) = 0 i.e
'( ) = . Supposons que ' possède deux points …xes 1 ; 2 2 [a; b] avec
'( 1 )j k j 2
k j 2
1 6= 2 alors j'( 2 )
1 j d’où j 2
1j
1 j alors
1 k : contradiction, donc 1 = 2 .
ii) On a jxn
j = j'(xn 1 ) '( )j k jxn 1
j ::: k n jx0
j,
n
comme 0 k < 1 donc lim k = 0 d’où lim xn = .
n!+1
n!+1
On a jxn+p xn j k jxn 1+p xn 1 j ::: k n jxp
jxp xp 1 j + jxp 1 xp 2 j + :::: + jx1 x0 j et jxi xi 1 j
::: k i 1 jx1 x0 j
3
x0 j et jxp x0 j
k jxi 1 xi 2 j
donc jxp
1
1
k
jx1
obtient j
(k p
x0 j
1
x0 j ainsi jxn+p
xn j
k
n
+ kp
xn j
2
+ ::: + 1) jx1
kn
1
k
jx1
x0 j =
kp
1
k
jx1
x0 j
x0 j et quand p ! +1 on
jx1 x0 j.
1 k
–Détermination pratique de la constante k
Si ' 2 C 1 ([a; b]), la formule des accroissements …nis s’écrit : pour tous
x; y 2 [a; b], il existe c 2 [x; y] ou [y; x] tels que '(x) '(y) = (x y)'0 (c).
Ainsi j'(x) '(y)j = j(x y)j j'0 (c)j j(x y)j max j'0 (t)j.
t2[a;b]
k = max j'0 (t)j
Prendre
t2[a;b]
– Application du théorème du point …xe à la résolution numérique de
f (x) = 0
Soit f (x) = 0 une équation où x 2 [a; b], alors on introduit une nouvelle
fonction ' telle : 8x 2 [a; b]; f (x) = 0 () '(x) = x. Ainsi les zéros de
f sont exactement les points …xes de ' et on applique alors la méthode du
point …xe à '.
Exemple : Soit f (x) = 2x e x où x 2 [0; 1]. On a f (0) = 1; f (1) =
2 e 1 = 1; 63:::et f 0 (x) = 2 + e x > 0 donc 9! 2 [0; 1] tel que f ( ) = 0.
Pour tout x 2 [0; 1], on a :
1
f (x) = 0 () 2x = e x () x = e x () x = '(x) avec
2
1 x
'(x) = e
2
1 x
i) On a '0 (x) =
e < 0, pour tout x 2 [0; 1] donc ' est décroissante
2
sur [0; 1].
1
1
Comme '(0) = 2 [0; 1] et '(1) =
= 0; 18::: 2 [0; 1] donc ' est stable
2
2e
sur [0; 1].
1
ii) Posons g(x) = j'0 (x)j = e x , cherchons le max de g sur [0; 1].
2
1 x
0
On a g (x) =
e
< 0 donc g est décroissante sur [0; 1] ainsi
2
1
max g(x) = g(0) = :
x2[0;1]
2
Donc ' est contractante sur [0; 1].
Conclusion : La méthode du point …xe est applicable à ' sur [0; 1] et la
suite xn+1 = '(xn ) converge vers et ceci pour tout x0 2 [0; 1].
4
V) Méthode de Newton (ou de la tangente)
Dé…nition : On appelle méthode de Newton pour la résolution
8 numérique
x0 2 [a; b]
<
f (xn )
de l’équation f (x) = 0 sur l’intervalle [a; b], le processus itératif
: xn+1 = xn
f 0 (xn )
0
avec f 6= 0.
–Interprétation géométrique :
Soit x0 2 [a; b], soit ( 0 ) la droite tangente à la courbe de f au point
(x0 ; f (x0 )) et soit f(x0 ; 0)g = ( 0 ) \ (xx0 ) où (xx0 ) est l’axe des abscisses.
-Exprimons x1 en fonction de x0
L’équation de la droite ( 0 ) est : y f (x0 ) = f 0 (x0 ) (x x0 )
comme f(x0 ; 0)g = ( 0 ) \ (xx0 ) donc f (x0 ) = f 0 (x0 ) (x1 x0 )
f (x0 )
.
d’où x1 = x0
f 0 (x0 )
f (x1 )
De la même façon, on retrouve x2 = x1
et par suite xn+1 =
f 0 (x1 )
f (xn )
xn
.
f 0 (xn )
Théorème : Soit f : [a; b] ! R une fonction de classe C 2 ([a; b]). Supposons
que
i) f (a) f (b) < 0
ii) 8x 2 [a; b]; f 0 (x) 6= 0
iii) f 00 garde un signe constant sur [a; b]
f (c)
a si jf 0 (a)j jf 0 (b)j
iv)
b
a
avec
c
=
b sinon
f 0 (c)
f (xn )
converge
Alors la suite récurrente (xn ) dé…nie par xn+1 = xn
f 0 (xn )
vers l’unique zéro de f sur [a; b] et ceci pour tout x0 de [a; b].
L’erreur d’approximation véri…e
M2
j
jxn xn 1 j2 , 8n 1
n = jxn
2m1
avec M2 = max jf 00 (x)j et m1 = min jf 0 (x)j.
x2[a;b]
x2[a;b]
Propriété
i) Si f 0 et f 00 sont du même signe sur [a; b] alors c = a
ii) Si f 0 et f 00 sont de signes contraires sur [a; b] alors c = b
Exemple : Soit f (x) = ex 4x où x 2 [0; 1]. On a
i) f (0) = 1 et f (1) = e 4 = 1; 28::: donc f (0)f (1) < 0
5
ii) f 0 (x) = ex 4 e 4 < 0 sur [0; 1]
iii) f 00 (x) = ex 0 sur [0; 1]
e 4
f (1)
=
= 1 b a = 1.
iv) f 0 f 00 < 0 donc c = b = 1 et
0
f (1)
e 4
Conclusion : la méthode de Newton est applicable à f sur [0; 1] et la suite
f (xn )
xn+1 = xn
converge vers l’unique zéro de f sur [0; 1] et ceci pour
f 0 (xn )
tout x0 de [0; 1].
6