modelisation mcc

MOTEUR A COURANT CONTINU 1/6
Modélisation d’un moteur à courant continu.
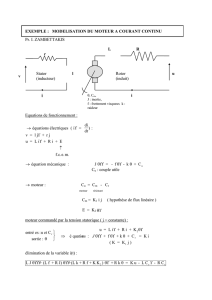
Un moteur à courant continu commandé par l’induit est utilisé pour commander en vitesse
un axe de robot.
Le schéma fonctionnel décrivant le fonctionnement du moteur est le suivant:
Les équations différentielles régissant le comportement du moteur sont:
)t(.a)t(Cf )t(i.Kc)t(Cm
)t(.K)t(e
)t(Cr)t(Cf)t(Cm
dt
d
.J
dt
di
.L)t(i.R)t(e)t(u
e
w=
=
w=
--=
w
++=
avec les notations suivantes:
u : tension aux bornes de l’induit en V
i : courant dans l’induit en A
R : resistance aux bornes de l’induit R=0.1 W
L : inductance aux bornes de l’induit L=0,5 mH
e : force électro-motrice en V
J : moment d’inertie J=0.01 kg.m²
Cf :couple de frottement en m.N
a : coefficient de frottement visqueux en m.N.rad-1.s
Cm : couple moteur en m.N
Cr : couple résistant en m.N
Ke : constante de f.e.m. Ke =0,1 V/rd/s
Kc : constante de couple Kc =0,1 Nm/A
w : pulsation de rotation du moteur en rad.s-1
Cr

MOTEUR A COURANT CONTINU 2/6
MOTEUR A COURANT CONTINU
I. Equations :
(1) )t(e
dt
di
L)t(Ri)t(u ++= (I) )p(E)p(I)LpR()p(U
+
+
=
(2) )t(Cr)t(Cf)t(Cm
dt
d
J--=
w
(II) )p(C)p(C)p(C)p(Jp rfm
-
-
=
W
(3) )t(Ke)t(e
w
=
(III) )p(Ke)p(E
W
=
(4) )t(iK)t(C cm
=
(IV) )p(IK)p(C cm
=
(5) )t(a)t(C f
w
=
(V) )p(a)p(C f
W
=
(6)
dt
d
)t(
q
=w (VI) )p(p)p(
Q
=
W
II. Schéma Bloc :
III. Fonction de transfert :
3.1. Couple résistant nul : Cr(t)=0èCr(p)=0
(II) et (V) è
aJp )p(C
)p(
m
+
=W
; (IV)è aJp )p(KcI
)p( + =W è)p(
KcaJp
)p(I W
+
=
(I) et (III) è )p(Ke)p(I)LpR()p(U
W
+
+
=
Kc KeKc)LpR)(aJp(
)p()p(Ke)p(
Kc )LpR)(aJp(
)p(U
+
+
+
W=W+W
+
+
=
2
JLpp)aLRJ(aRKeKc
Kc
)LpR)(aJp(KeKc Kc )p(U )p(
)p(H ++++ =
+++
=
W
=
2
0
2
0
2
p
p
2
1
K
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(U )p(
)p(H
w
+
w
x
+
=
+
+
+
+
+
+
=
W
=
Fonction de transfert du deuxième ordre, de classe 0 avec :
aRKeKc
Kc
K+ = : gain statique en rad.s-1.V-1,
aRKeKc
JL12
0+
=
w
èJL aRKeKc 0+ =w pulsation propre du système en rad.s-1,
aRKeKc aLRJ2 0 +
+
=
w
x
è aRKeKc aLRJ
2
0
+
+
w
=x amortissement du système (sans unité).
U(p)
E(p)
LpR 1 +
I(p) Kc Cm(p)
Cr(p)
Cf(p)
Jp
1
Ω(p)
p
1
a
Ke
Θ(p)
H(p)
U(p) Ω(p)

MOTEUR A COURANT CONTINU 3/6
Cas particuliers : Cf et L négligeables
Tp1 K
p
KeKc
RJ
1
Ke
1
)p(U )p(
)p(H + =
+
=
W
=
Fonction de transfert du premier ordre, de classe 0 avec :
Ke
1
K= : gain statique en rad.s-1.V-1,
KeKc
RJ
T= constante de temps du système en s.
Applications numériques :
Kc=0.1m.N.A-1, Ke=0.1 V.rad-1.s-1,R=0.1Ohm, a=0, L=0.5mH et J=0.01kg.m2
Remarque : Ke et Kc sont souvent égaux ( en valeurs numériques )
Ke peut être à calculer à partir d’une valeur de ω et de e :
Exemple : pour une vitesse de N=1000tr/min, e=100V
11
srad.V955.0
7.104
100
Kes/rad7.104
60
1000*2
--
==®=
P
=w
Cas général :
10
1.0*1.0 1.0 aRKeKc
Kc
K==
+
= rad.s-1.V-1 : gain statique,
7.445202000
10.5.0*01.0
1.0*1.0
JL aRKeKc
3
0 ====
+
=w
- rad.s-1
pulsation propre du
système,
23.25
01.*1.0 01.0*1.0 2520 ===x
amortissement du système (sans unité).
Donc
2000
p
p
10
p
1
10
)p(U )p(
)p(H 2
++
==
W
=
, deuxième ordre, de classe 0.
Cas particuliers : L négligeable
10
1.01 Ke
1
K=== rad.s-1.V-1 : gain statique,
1.0
1.0*1.0 01.0*1.0 KeKc
RJ
T=== s constante de temps du système.
10
p
1
10
)p(U )p(
)p(H
+
==
W
= , premier ordre, de classe 0.

MOTEUR A COURANT CONTINU 4/6
3.2. Couple résistant non nul :
(II) et (V) è )p(Cr)p(C)p()aJp( m
-
=
W
+
; (IV)è )p(Cr)p()aJp()p(KcI
+
W
+
=
(I) et (III) è )p(Ke)p(I)LpR()p(U
W
+
+
=
)p(Ke
Kc )p(Cr)p()aJp(
)LpR()p(U W+
+
W
+
+=
)p(
Kc KeKc)aJp)(LpR(
)p(Cr
Kc )LpR(
)p(U W
+
+
+
=
+
-
)p(Cr
KeKc)aJp)(LpR( )LpR(
)p(U
KeKc)aJp)(LpR( Kc
)p( +++
+
-
+++
=W
)p(Cr
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKcLpR
)p(U
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(
22
+
+
+
+
+
+
+
-
+
+
+
+
+
+
=W
2
1
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(H)p(H
+
+
+
+
+
+
==
et
2
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKcLpR
)p(2H
+
+
+
+
+
+
+
=
Cas particuliers : Cf et L négligeables
p
KeKc
RJ
1
Ke
1
)p(H)p(H 1
+
==
et
p
KeKc
RJ
1
KeKc
R
)p(2H
+
=
H(p)
U(p) Ω(p)
H1(p)
U(p)
Cr(p) H2(p)
Ω(p) )p(Cr)p(H)p(U)p(H)p(
21
-
=
W
Cr(p)

MOTEUR A COURANT CONTINU 5/6
I.V. Réponse à un échelon de tension : u(t)=U0 è
p
U
)p(U
0
=
4.1. Fonction de transfert du deuxième ordre : la réponse dépend de la valeur de ξ.
si ξ>1 : régime apériodique,
si ξ=1 : régime critique,
si ξ<1 : régime pseudo périodique.
4.1.1. Couple résistant nul :
p
U
.
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(U
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(
0
22
+
+
+
+
+
+
=
+
+
+
+
+
+
=W
0
0
2
0p0pt
U
aRKeKc
Kc
p
U
.
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
plim)p(plim)t(lim)( + =
+
+
+
+
+
+
=W=w=¥w
®®¥®
En régime permanent : 00 KUU
aRKeKc
Kc
)( =
+
=¥w
A.N. : U0=10V, K=10 rad.s-1.V-1è100)(
=
¥
w
rad.s-1è min/tr955
*2 100*60
N=
p
=
23.25 ===x è régime apériodique.
4.1.2. Couple résistant non nul : Cr(t)=C0è
p
C
)p(Cr
0
=
p
C
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKcLpR
p
U
p
aRKeKc
JL
p
aRKeKc aLRJ
1
aRKeKc
Kc
)p(
0
2
0
2
+
+
+
+
+
+
+
-
+
+
+
+
+
+
=W
00
0pt C
aRKeKc
R
U
aRKeKc
Kc
)p(plim)t(lim)( ++ =W=w=¥w -
®¥®
A.N. : U0=10V, K=10 rad.s-1.V-1, C0=5m.N, 10
aRKeKc
R=
+
rad.s-1. m-1.N-1
100)(
=
¥
w
-50=50 rad.s-1è min/tr5.477
*2 50*60
N=
p
=
ξ<1
ξ>1
ξ =1
ω(t)
t