ECS2-Chapitre10a

Variables aléatoires à densité
Chapitre 10a
1 Généralités sur les variables aléatoires à den-
sité 2
1.1 Définition .................... 2
1.2 Densité de probabilité . . . . . . . . . . . . . 4
1.3 Variable aléatoire fonction d’une variable
aléatoire à densité . . . . . . . . . . . . . . . 6
2 Moments d’une variable aléatoire à densité 8
2.1 Espérance.................... 8
2.2 Théorème de transfert . . . . . . . . . . . . . 10
2.3 Moments d’ordre supérieur, variance . . . . . 11
Compétences attendues.
3Prouver qu’une variable aléatoire Xest à densité.
3Montrer qu’une fonction fest une densité de probabilité.
3Déterminer la fonction de répartition d’une variable aléatoire Y=g(X).
3Déterminer une densité d’une variable aléatoire X.
3Prouver l’existence et calculer une espérance ou une variance d’une variable à densité.
3Utiliser le théorème de transfert pour calculer une espérance.
Mathieu Mansuy - Professeur de Mathématiques en ECS2 au Lycée Louis Pergaud (Besançon)
[email protected]

ECS2 Lycée Louis Pergaud
1 Généralités sur les variables aléatoires à densité
Dans tout ce chapitre, (Ω,A, P )désigne un espace probabilisé.
1.1 Définition
Rappels.
•On appelle fonction de répartition d’une variable aléatoire réelle Xla fonction FXdéfinie sur R
par :
∀x∈R, FX(x) = P(X≤x).
•Une application F:R→Rest la fonction de répartition d’une variable aléatoire réelle Xsi et
seulement si elle satisfait les points suivants :
(i) Fest croissante sur R;
(ii) Fest continue à droite en tout point de R;
(iii) lim
x→−∞ F(x)=0et lim
x→+∞F(x)=1.
De plus, on a l’égalité :
∀x∈R, P (X=x) = P(X≤x)−P(X < x) = F(x)−lim
t→x−
F(t).
Définition.
Soit Xune variable aléatoire réelle sur (Ω,A, P ). On dit que Xest une variable aléatoire à densité
(ou variable aléatoire continue) si sa fonction de répartition FXest de plus :
(iv) continue sur R;
(v) de classe C1sur Réventuellement privé d’un nombre fini de points.
Remarque. Les trois courbes suivantes sont celles de fonctions de répartition de variables aléatoires
réelles.
•La courbe bleu est en escalier. C’est donc la fonction de répartition d’une variable discrète X.
Rappelons qu’elle est discontinue à droite en tout point de son support X(Ω). En particulier,
une variable discrète n’est donc pas à densité.
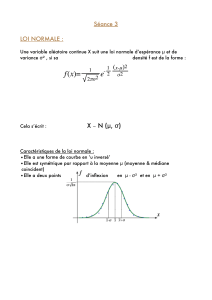
•La courbe rouge représente une fonction de répartition (celle de la loi normale N(0,1)) de classe
C1sur R. C’est donc la fonction de répartition d’une variable continue.
2

ECS2 Lycée Louis Pergaud
•La fonction représentée par la courbe noir est discontinue en certains points, et n’est pas en
escalier. C’est la fonction de répartition d’une variable aléatoire qui est ni discrète, ni continue.
Cette année nous n’étudierons pas ce type de variables aléatoires, on se focalisera sur les cas
discret et continue.
Exercice. On considère la fonction F:R→Rdéfinie pour tout x∈Rpar F(x) = (0si x < 0
1−e−λx si x≥0.
1. Représenter graphiquement la fonction F.
2. Montrer qu’il existe une variable aléatoire Xdéfinie sur l’espace probabilisé (Ω,A, P )de fonction
de répartition F.
On dit qu’une telle variable aléatoire suit une loi exponentielle de paramètre λet on note
X →E(λ).
3. Montrer que Xest une variable aléatoire continue.
3

ECS2 Lycée Louis Pergaud
1.2 Densité de probabilité
Définition.
Soit Xune variable aléatoire à densité.
On appelle densité de probabilité de Xtoute fonction fsatisfaisant les deux points suivants :
(i) fest positive sur R;
(ii) f(x) = F0
X(x)pour tout xappartenant à Réventuellement privé d’un nombre fini de points.
Remarque. Une densité d’une variable aléatoire n’est pas unique : si fest une densité de Xet si
l’on change la valeur de fen un nombre fini de points (en prenant pour nouvelles valeurs des réels
positifs) alors on obtient une autre densité de f. Ainsi on parlera pour fd’une densité de Xet non
de la densité de X.
Exercice. Soit λ > 0et X →E(λ). Déterminer une densité de X.
Soit Xune variable aléatoire à densité, et fXune densité de X. Pour tout x∈R, l’intégrale
Zx
−∞
fX(t)dtconverge et on a :
FX(x) = P(X≤x) = Zx
−∞
fX(t) dt.
Propriété 1 (Lien fonction de répartition/densité)
Remarque. La donnée d’une densité d’une variable aléatoire caractérise donc sa loi. En particulier si
Xet Ysont à densité de densités respectives fXet fY, elles ont même loi si et seulement si fX=fY
sauf en un nombre fini de points.
Soit Xune variable aléatoire à densité, et fXune densité de X. On a :
•∀a∈R,P(X=a)=0.
•∀a, b ∈R,P(a≤X≤b) = P(a≤X < b) = P(a<X≤b) = P(a < X < b).
•∀a, b ∈R,P(a≤X≤b) = Zb
a
fX(t)dt.
Propriété 2 (Lien probabilités/densité)
4

ECS2 Lycée Louis Pergaud
Preuve. Fétant continue, on a pour tout a∈R:
P(X=a) = F(a)−lim
x→a−
F(x)=0.
Ainsi pour tout a, b ∈R, on a P(a≤X≤b) = P(X=a) + P(a<X≤b) = P(a<X≤b). On
démontre de même les autres égalités. On a enfin :
P(a≤X≤b) = P(a<X≤b) = P(X≤b)−P(X≤a) = F(b)−F(a) = Zb
a
fX(t) dt.
Ainsi si Xest continue, P(X=a)=0pour tout a∈R. Ceci est bien évidemment faux lorsque
Xest une variable aléatoire discrète.
Mise en garde.
Soit fune fonction de Rdans R.fest une densité d’une variable aléatoire si et seulement
si elle satisfait les points suivants :
•fest continue sur Rsauf éventuellement en un nombre fini de points ;
•fest positive sur R;
•Z+∞
−∞
f(t) dt converge et vaut 1.
Propriété 3
Exercice. Soit λ∈R. Pour tout t∈R, on pose f(t) = λ
1 + t2.
a) Déterminer la valeur de λpour que fsoit une densité d’une variable aléatoire X.
On dit que Xsuit une loi de Cauchy.
b) Déterminer sa fonction de répartition FX.
c) Tracer les courbes représentatives de fet FXet représenter graphiquement les probabilités
P(−1≤X≤1) et P(X≥1). Calculer ces probabilités. Que vaut P(X≤ −1) ?
5