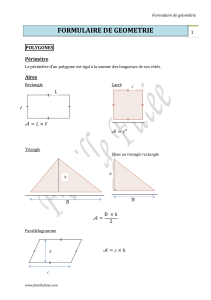
cours de maths TS

COURS DE MATHÉMATIQUES
Terminale S
Valère BONNET (valere.[email protected])
29 mai 2011
Lycée PONTUS DE TYARD
13 rue des Gaillardons
71100 CHALON SUR SAÔNE
Tél. : [phone]
Fax : [phone]
FRANCE

ii
LYCÉE PONTUS DE TYARD Terminale VI

Table des matières
Table des matières iii
I Vocabulaire de la logique 1
I.1 Qu’est-ce qu’une proposition ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
I.2 Négation d’une proposition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
I.3 Le « et » . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
I.4 Le « ou » . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
I.5 Propositions et parties d’un ensemble . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
I.6 Lois de MORGAN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
I.7 Opérations sur les parties d’un ensemble . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
I.8 Implications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
I.8.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
I.8.2 Réciproque d’une implication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
I.8.3 Contraposée d’une implication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
I.8.4 Implication contraire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
I.9 Double implication ou équivalence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
I.10 Formules récapitulatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
I.11 Raisonnement par récurrence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
II Révisions 9
II.1 Identités remarquables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
II.2 Éléments de symétries d’une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
II.2.1 Symétries dans IR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
II.2.2 Axe de symétrie d’une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
II.2.3 Centre de symétrie d’une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
II.3 Trigonométrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
II.3.1 Quelques valeurs remarquables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
II.3.2 Quelques formules . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
II.3.3 Équations trigonométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
II.4 Géométrie du triangle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
II.4.1 Aire d’un triangle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
II.4.2 Théorème des sinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
II.4.3 Théorème d’ALKASHI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
II.4.4 Théorème de la médiane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
II.5 Polynômes du second degré . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
II.5.1 Forme canonique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
II.5.2 Représentation graphique et sens de variation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
II.5.3 Factorisation et résolution d’équations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
II.5.4 Signe d’un trinôme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
II.5.5 Tableau récapitulatif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
II.5.6 Compléments . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
II.5.7 Travaux dirigés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
II.5.8 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
II.6 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
iii

iv Table des matières
III Suites numériques 31
III.1 Vocabulaire de l’ordre dans IR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
III.1.1 Majorants, minorants .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
III.1.2 Théorème de la borne supérieure (complément) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
III.2 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
III.2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
III.2.2 Composée d’une suite par une fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
III.2.3 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
III.3 Représentation graphique d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
III.3.1 Représentation graphique d’une suite définie explicitement ...................... 32
III.3.2 Représentation graphique d’une suite définie par récurrence ..................... 33
III.3.3 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
III.4 Suites bornées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
III.4.1 Généralités . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
III.4.2 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
III.5 Suites monotones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
III.5.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
III.5.2 Méthodes d’étude du sens de variation d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
III.5.3 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
III.6 Suites arithmétiques - suites géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
III.6.1 Suites arithmétiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
III.6.2 Suites géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
III.6.3 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
III.7 Limites de suites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
III.7.1 Limite finie, limite infinie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
III.7.2 Théorèmes de comparaisons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
III.7.3 Calcul algébrique de limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
III.7.4 Limites de suites géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
III.7.5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
III.8 Suites monotones bornées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
III.8.1 Théorème de convergence d’une suite monotone . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
III.8.2 Suites adjacentes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
III.8.3 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
III.8.4 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
III.9 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
IV Limites de fonctions, continuité 53
IV.1 Limite finie (ou réelle) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
IV.1.1 Limite d’une fonction en +∞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
IV.1.2 Limite d’une fonction en un réel a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
IV.2 Notion de continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
IV.3 Utilisation de la continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
IV.3.1 Continuité et bijection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
V Exponentielles et équations différentielles 57
V.1 La fonction exponentielle de base e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
V.1.1 Propriété fondamentale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
V.1.2 Sens de variation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
V.1.3 Autres propriétés algébriques de l’exponentielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
V.1.4 Quelques limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
V.2 La fonction logarithme népérien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
V.2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
V.2.2 Dérivabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
V.2.3 Dérivée de lnu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
V.2.4 Logarithme népérien et calcul intégral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
V.3 Des exponentielles et des logarithmes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
V.3.1 Notation ab, pour a,bréels et a>0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
V.3.2 Fonctions exponentielles de base a(avec a>0) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
V.3.3 Fonctions logarithmes de base a(avec a>0 et a,1) . . . . . . . . . . . . . . . . . . . . . . . . . . 63
V.4 Équations différentielles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
V.4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
LYCÉE PONTUS DE TYARD Terminale VI

Table des matières v
V.4.2 Équations du type y′−ay =0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
V.4.3 Équations du type y′−ay =b. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
V.4.4 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
VI Dérivabilité 69
VI.1 Fonctions dérivables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
VI.1.1 Nombre dérivé, fonction dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
VI.1.2 Dérivabilité des fonctions usuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
VI.1.3 Principaux résultats . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
VI.2 Dérivation d’une fonction composée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
VI.2.1 Théorème de dérivation d’une fonction composée . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
VI.2.2 Dérivée de la fonction pu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
VI.2.3 Dérivée de la fonction un(n∈). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
VI.3 Dérivation et études de fonctions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
VI.3.1 Sens de variation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
VI.3.2 Extremum local . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
VI.4 Dérivées successives d’une fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
VI.5 Exercices résolus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
VII Nombres complexes 77
VII.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
VII.1.1 Des équations et des ensembles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
VII.1.2 Activités . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
VII.1.3 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
VII.1.4 Calcul dans . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
VII.2 Interprétations géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
VII.2.1 Affixe, point image, vecteur image . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
VII.2.2 ~ u+~ u′,k~ u,~ MM′. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
VII.2.3 Écriture complexe de certaines symétries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
VII.2.4 Coordonnées polaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
VII.2.5 Module et arguments . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
VII.3 Propriétés algébriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
VII.3.1 Propriétés du conjugué . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
VII.3.2 Propriétés du module et des arguments . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
VII.3.3 Formule de MOIVRE (complément) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
VII.4 Notation exponentielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
VII.4.1 Une équation différentielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
VII.4.2 Définitions et propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
VII.4.3 Forme exponentielle et symétries usuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
VII.4.4 Formules d’EULER . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
VII.4.5 Racines carrées d’un nombre complexe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
VII.5 Nombres complexes et polynômes (compléments) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
VII.5.1 Théorème fondamental de l’algèbre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
VII.5.2 Résolution des équations du second degré . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
VII.6 Utilisation des nombres complexes (compléments) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
VII.6.1 Racines n-ièmes de l’unité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
VII.6.2 Racines n-ièmes d’un nombre complexe non nul . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
VII.6.3 Polynômes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
VII.6.4 Forme algébrique des racines carrées d’un nombre complexe ..................... 92
VII.6.5 Trigonométrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
VII.7 Géométrie et nombres complexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
VII.7.1 Propriétés générales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
VII.7.2 Écriture complexe de quelques transformations usuelles ........................ 95
VII.7.3 Affixe du barycentre d’un système de points pondérés . . . . . . . . . . . . . . . . . . . . . . . . . . 96
- série S