CINEMATIQUE DU POINT SI 2020 - 1 -
La Cinématique analytique permet à partir d’équations de définir à tout instant, la position, la
vitesse et l’accélération d’un point en fonction du mouvement du solide auquel il appartient.
1 - GENERALITES
Quelle que soit l’étude
cinématique, on a toujours
besoin de se situer dans le
temps. On appelle instant t
ou date t le temps écoulé
depuis une origine des temps
t0=0, choisie arbitrairement.
L’unité de mesure du temps
(système ISO) est la
seconde, notée s.
t = t2-t1 est appelée durée entre les deux instants t1 et t2.
1.1 Vitesse :
➢ La vitesse moyenne (vmoy) est le rapport de la distance parcourue sur un intervalle de temps
plus ou moins long
➢ La vitesse instantanée (v) est le rapport de la distance parcourue sur un intervalle de temps
infiniment petit
1.2 Accélération :
➢ L’accélération moyenne (amoy) est le rapport de la variation de vitesse sur un intervalle de
temps plus ou moins long
➢ L’accélération instantanée (a) est le rapport de la variation de vitesse sur un intervalle de temps
infiniment petit
➢ L’accélération est positive, si le mouvement est accéléré (accélération dans le sens du mouvement)
➢ L’accélération est négative, si le mouvement est décéléré ou ralenti (accélération opposée au
mouvement)
De cette manière un solide lâché d’une hauteur x0 à un temps t0, sans vitesse initiale ne serait
soumis qu’à l’accélération de la pesanteur (constante), soit g = 9,81 m.s-2 :
-au temps t0 +1 seconde, ce solide atteindrait une vitesse instantanée de 9,81 m.s-1
-au temps t0 +2 secondes, ce solide atteindrait une vitesse instantanée de 9,81 x 2 soit 19,62 m.s-1
1.3 Unités du S.I :
• Position notée x exprimée en m
• Temps noté t exprimée en s
• Vitesse notée v exprimée en m.s-1
• Accélération notée a exprimée en m.s-2

CINEMATIQUE DU POINT SI 2020 - 2 -
a : accélération du solide en m.s-2
v0 : vitesse initiale du solide en m.s-1
x0 : position initiale du solide en m
x : Position d’un point à un instant t.
x0
x
v
a
0
t
t
t
V0
α
tanα = v0
x = v0t + x0
0
0
v = v0 = cte
a= 0
X(t) = v0 . t + x0
v(t) = v0 = Constante
a(t) = 0
2 - TRANSLATION RECTILIGNE
REPERAGE ESPACE & TEMPS :
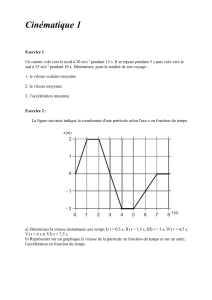
2.1 Vitesse constante : Mouvement Rectiligne Uniforme (MRU) :
➢ Définition : Un solide est en MRU si :
• la trajectoire de chacun de ses points est une droite,
• sa vitesse est constante (a = 0).
Equations horaires :
➢ Étudions une voiture qui roule à vitesse constante sur une route rectiligne.
Mouvement Rectiligne Uniforme (MRU) : Vitesse constante
MRU

CINEMATIQUE DU POINT SI 2020 - 3 -
Remarque : On peut déduire de ces 2 équations une formule utile :
)(2
22 xoxavov−+=
x0
x
v
a
0
t
t
t
V0
x =
00
2xtvta
2
1++
0
0
v = a.t + v0
a= cte
Branche de parabole
2.2 Si Vitesse variable et accélération constante :
Mouvement Rectiligne Uniformément Varié (MRUV) :
Equations horaires :
➢ Reprenons notre même véhicule. Le conducteur décide d’appuyer (raisonnablement)
sur l’accélérateur :
Mouvement Rectiligne Uniformément Varié (MRUV) :
votaxv +== .'
cstexva === '''
𝑥 = 1
2𝑎. 𝑡²+𝑣𝑜. 𝑡 + 𝑥𝑜
MRUV

CINEMATIQUE DU POINT SI 2020 - 4 -
(t) = 0 . t + 0
(t) = 0 = Constante
’(t) = 0
’ : accélération angulaire du solide en rad.s-2
0 : vitesse angulaire initiale du solide en rad.s-1
0 : position angulaire initiale du solide en rad
: Position angulaire d’un point à un instant t.
Remarque : On peut déduire de ces 2 équations une formule utile :
)('2
22 oo
−+=
0
+
=t
Accélération
Décélération ou
freinage
vitesse constante : (at=0)
α > 0
α < 0
α = 0 ; at = 0 ; ω = cte et vA = cste
vA
O
α
ω
TA
x
A
at
an
aA
r
vA
vA
O
ω
TA
x
A
an
r
vA
vA
vA
A
O
α
ω
TA
x
A
at
an
aA
r
vA
vA
vA
3 - ROTATION AUTOUR D’UN AXE FIXE
3.1 Vitesse angulaire constante : Mouvement Circulaire Uniforme (MCU) :
➢ Définition :
Un solide est en MCU si :
• la trajectoire de chacun de ses points est un cercle,
• sa vitesse est constante (’ = 0).
➢ Rappel :
60 N2.
ω
=
Si N est la vitesse de rotation en tours par minute alors :
On remarquera que : 1 tr/min = 0,1047 rad/s
Avec : ω en rad/s et N en tr/min.
Equations horaires :
3.2 Si accélération angulaire constante : Mouvement Circulaire Uniformément Varié (MCUV) :
Equations horaires :
00
²
2
1
++
=tt
cste''' ==
MCUV
MCU
1
/
4
100%