Grandeurs fondamentales (1)

I - 2 ) Grandeurs sinusoïdales ( AC ou ) :
Une grandeur sinusoïdale s’exprime par :
est l’amplitude du signal, est la pulsation, et est la phase à l’origine des temps.
Remarque : En électrotechnique, on prend la phase à l’origine des temps de la tension nulle, on
aura :
est le déphasage du courant sur la tension; il s’agit d’un retard algébrique qui est positif pour
les récepteurs inductifs, négatif pour les récepteurs capacitifs.
)sin(2S ) sin(S s(t) effmax  tt
Smax
)(cos2I i(t)et )cos(2V v(t)  tt
2
a - Représentation complexe des courants et des tensions alternatifs sinusoïdales :
On représente une grandeur sinusoïdale, dans le plan complexe, par son module et sa phase.
On aura l’équivalence suivante :
* Grandeurs temporelles :
)( cos2I )t(iet )cos(2V v(t)  tt
2 0
)i(
inductif dipole : 0
) v(
t

* Grandeurs complexes associées :
On représente ces complexes dans le plan complexe ( appelé aussi diagramme de Fresnel ) sous
la forme :
Dipôle inductif Dipôle capacitif
)exp(-jI Iet V V
3
0
0
Re Re
I
I
Im Im
V
V
b–Récepteurs électriques :
En régime alternatif quelconque, il existe trois types de dipôles : les résistances, les inductances
et les capacités. A chacun de ces dipôles correspond une relation liant la tension à ses bornes et
le courant qui le traverse :
-Pour la résistance :
-Pour l’inductance :
-Pour la capacité :
v
dt
dv
C (t) i
dt
di
L (t) v
(t) iR (t) v
i
iR
v
L
v
C
i

En utilisant la notation complexe, les relations courant tension des dipôles deviennent :
4
I
V
jC
1
VjC I
I
V
jL IjL V
I
V
R IR V
La grandeur, notée : est appelée impédance.
I
V
Z 
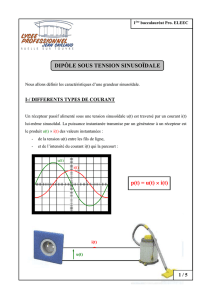
II –Les puissances électriques:
II –1 ) La puissance active:
Un dipôle électrique placé sous une tension de valeur efficace V et parcouru par un courant de
valeur efficace I consomme une puissance P , dite active, toujours inférieure ou égale au
produit V.I , on écrit alors en convention récepteur : P = k .V. I ou 0≤ k ≤ 1.
facteur de puissance.
P > 0 : correspond à une puissance consommée par le dipôle.
P < 0 : correspond à une puissance fournie par le dipôle.
II- 2 ) Puissance électrique en alternatif sinusoïdal :
On considère le cas général le plus répandu en électrotechnique d’un dipôle inductif, c-à-d d’un
courant déphasé en arrière d’un angle par rapport à la tension :
Le facteur k est appelé :
)(cos2I i(t)et )cos(2V v(t)  tt

5
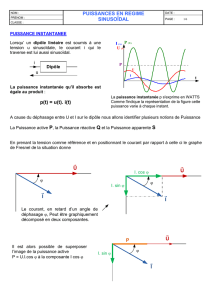
La puissance instantanée est définit par :
C-à-d :
i(t) v(t) p(t) 
)(2 cosIV )( cosIV (t) p  t
b –Puissance active :
C’est la valeur moyenne de la puissance instantanée, c-à-d : < >
c –Puissance apparente :
Les grandeurs v(t) et i(t) étant périodiques, on les caractérisent par leurs valeurs efficaces
Vet I.
On définit alors la puissance apparente comme la grandeur nommée S: S = V . I (en VA ).
d –facteur de puissance :
En alternatif sinusoïdal , le facteur de puissance est défini comme la grandeur sans unité :
cosIV p(t) P 
cos
S
P
k 
e –Puissance réactive :
On définit la puissance réactive par : . Son unité est le Volt Ampère Réactif (VAR)
sin IV Q 
a –Puissance instantanée :

D’autre part, on fait également apparaitre la grandeur
caractéristique :
g –Puissance apparente complexe :
Pour relier toutes ces grandeurs, en régime sinusoïdal , on peut faire apparaitre une grandeur de
calcul: la puissance apparente complexe, notée Squ’on définit comme suit :
P
Q
S
P
Q
tg 
6
Q j P IV :ou D'
sin IV j cos IV )(j exp IV IV : Donc
V Vet sin I j cos I )j( exp I I : Comme
) I de conjugé complexe leest I ( IV
*
*
**
S
On retrouve également que : S = S
On exprime dans le tableau ci-dessous les puissances absorbées par les différents récepteurs
fondamentaux de l’électrotechnique, en régime alternatif sinusoïdal :
f –Triangle des puissances :
Notons que :
Cette formule fait apparaitre également une relation graphique entre les différentes grandeurs.
On parle alors de triangle des puissances :
222 Q P S :ou d' IV Set sin IV Q , cos IV P