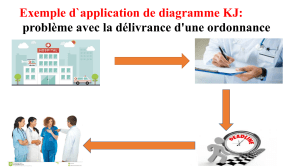
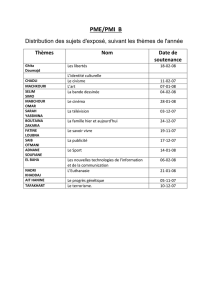
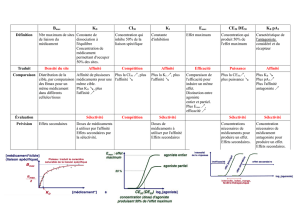
évolution d'un système chimique

Année :2019-2020 agp1 Seman Adnane
1
Chapitre : évolution d’un système chimique
Introduction :
Lorsque l’on considère un système fermé de plusieurs constituants physico-chimique plusieurs questions se
posent :
 Ce système va-t-il évoluer, si oui, dans quel sens ?
 Quel sera la composition de chacune des phases à l’équilibre ?
 Si l’opérateur changent l’une des variables d’état ou s’il ajoute un constituant comment le système
évolue ?
I)Affinité chimique d’un système :
1)Définition :
Considérons un système fermé dans lequel se déroule une seul réaction chimique d’équation
0
i
iiB
.
La différentielle de l’enthalpie libre G s’écrit :
i
iidnSdTVdpdG 
Soit en utilisant les variables de De Donder :
dSdTVdpdG iii
L’affinité chimique A a été définie par De Donder à partir de la relation :
pT
iiir G
GpTA
,
),,( 
De même l’affinité chimique standard a pour expression :
)()(),,( 0000 TTGpTA iiir 
La différentielle de l’enthalpie libre G s’écrit dans ce cas :
AdSdTVdpdG 
 Attention : l’affinité chimique est définie après l’écriture de l’équation de la réaction considérée.
2)Relation entre l’affinité et la création d’entropie interne :
Différentions la relation définissant l’enthalpie libre G d’un système au sein duquel se déroule une
transformation physico-chimique (réaction chimique, changement de phase) réversible ou non :
SdTTdSdHTSHddG  )(
Or :
VdppdVdUpVUddH  )(
Avec :
 WQdU
Soit :
SdTTdSVdppdVWQdG 
Dans le cas où le seul travail est le travail des forces de pression,
0
.
Supposons de plus que les échanges d’énergie et de travail entre le système et l’extérieur soient réversibles,
le système et le milieu sont en équilibre thermique (T=Te) et mécanique (p=pe).
La seule cause éventuelle d’évolution irréversible du système est alors la transformation physico-chimique
dont il est le siège. Dans ces conditions :
pdVdVPW e

Année :2019-2020 agp1 Seman Adnane
2
Et :
T
Q
SSSdS iei
Soit :
i
STTdSQ 
Où
i
S
représente la création d’entropie du système lors de son évolution par une transformation
irréversible.
L’expression générale précédente de dG se réécrit alors :
SdT– TdS– Vdp + pdV + pdV– ST– TdS =dG i
Soit, enfin :
i
ST– SdT–VdpdG 
D’après ce qui le paragraphe précédent on a :
AdSdTVdpdG 
Par identification on a :
0ST i Ad
3)condition d’évolution et d’équilibre :
a) condition d’évolution :
Si le système n’est pas en équilibre, il va, conformément au Deuxième Principe de la Thermodynamique,
évoluer de manière irréversible au cours d’une réaction physico-chimique. La création d’entropie doit être
positive
0Si
0 Ad
0 Gd
r
Un système dont l’affinité chimique est positive tend à évoluer dans le sens où l’avancement croît
)0(  d
c’est-à-dire dans le sens direct
1
Inversement, si l’affinité chimique est négative, le système tend à évoluer dans le sens inverse
2
.
b) condition d’équilibre :
Le système évolue tant que le critère
0 Ad
peut être satisfait. Il cesse d’évoluer si :
 A s’annule
)0(  G
r
le système est alors en équilibre physique et en équilibre chimique.
atteint l’une de ces bornes d =0 ; le réactif limitant ayant été entièrement consommé, le système
est en équilibre physique, mais pas en équilibre chimique, on dit qu’il y a rupture d’équilibre
chimique.
4) Affinité chimique et quotient de réactionnel Q :
Pour chaque constituant Ai, à un instant t :
iii aRT ln
0
L’enthalpie libre de réaction
G
r
en cours d’évolution est donc :
i
ii iiiii iir aRTaRTGln)ln(00  
 ii
v
i
aRTG
r
G
rln
0
 i
i
i
aRTG
r
G
r
ln
0

Année :2019-2020 agp1 Seman Adnane
3
On pose
i
i
i
aQ
QRTGG rr ln
0
or
GA r
donc
QRTAA ln
0
Or à l’équilibre
éqéq QRTAA ln
0
On note alors
)(
0TK
constante thermodynamique d’équilibre tel que :
)(ln)( 00 TKRTTA 
ou
0)(ln)( 00  TKRTTG
r
avec
iéqiéq i
aTKQ )()(
0
.
Lorsque l’équilibre est atteint (composition uniforme et invariante dans chaque phase) et si tous les
constituants de la réaction sont présents, le quotient réactionnel vérifie une constante d’équilibre,
indépendante de l’état initial, ne dépendant que de T.
Remarque :
)(
0TK
se calcule à partir des seules grandeurs standard.
)(
0TK
ne dépend pas de l’état initial et
RT TG
r
eTK
)(
0
0
)(
5) visualisation graphique *
:
Envisageons une évolution à T et p fixées d’un système chimique la fonction enthalpie libre G de ce
système à l’allure suivante :
Figure 1 : évolution du système
6) variation de
)(
0TK
avec la température :

Année :2019-2020 agp1 Seman Adnane
4
On a
RT
G
TK r0
0)(ln 
Or d’après Gibbs-Helmholtz :
2
00
TH T
G
dT
drr 
2
00 )()(ln RT TH
dT TKd r
cette relation est appelée
l’isobare de Vant’hoff.
II)variance-Déplacement ou rupture d’équilibre :
1)Facteurs d’équilibre-Variance :
a)Facteurs d’équilibre :
On appelle facteur d’équilibre tout paramètre dont la variation entraine une évolution du système.
 Remarque : Si une réaction est athermique
)0)(( 0 TH
r
, la température T est alors sans
influence.
 Si une réaction se fait à quantité gazeuse constante
)0(  gr
, la pression p sans influence.
 Par contre les paramètres de compositions sont toujours facteurs d’équilibre.
b) variance
La variance v correspond au nombre de paramètres intensifs indépendants que l’expérimentateur peut
choisir pour déterminer totalement l’état d’équilibre du système.
V=X-Y
X : nombre total de paramètre intensifs.
Y : nombre total de relations entre paramètres intensifs à l’équilibre.
Exemple :
Prenons la réaction de synthèse de l’ammoniac :
N2(g)+3H2(g)=2NH3(g)
A l’état initial nous disposons d’un mélange quelconque de N2, H2 et NH3, on dénombre 5 paramètre
intensifs T, P,
2
H
x
,
2
N
x
et
3
NH
x
; X=5.
Décomptons le nombre de relation :
1)
ii
x1
2)
ii
éq
i
xTK )()(
0
Y=2 ; Il en résulte v=3.
Si l’expérimentateur connait 3 paramètres il peut déduire les 2 autres.
 On peut calculer la variance on utilisons la règle des phases de Gibbs, la variance selon cette règle
est donné par :

Année :2019-2020 agp1 Seman Adnane
5
V=(N-r-K)+2-φ=C+2-φ
N :nombre de constituant physico-chimique.
r :nombre d’équilibre chimique
p :nombre de relation particulière
2 : T et p
Φ : nombre de phases ;
Remarque :
 Si T ou p est sans influence on parle de variance réduite et v=c+1-φ
 Connaissant la variance d’un système en équilibre chimique ou susceptible de l’être il est possible
de déterminer sans aucun autre calcul, si la modification de l’un des paramètres intensifs perturbera
ou non le système.
2)Déplacement ou rupture d’équilibre :
Dans un système en équilibre chimique, la modification d’un paramètre, intensif ou extensif, provoque
généralement une évolution du système vers un nouvel état d’équilibre. L’état d’équilibre final peut être
obtenu par :
• déplacement de l’équilibre initial, s’il correspond au même système physicochimique ;
• rupture d’équilibre, s’il ne correspond pas au même système physico-chimique (apparition ou disparition
d’une phase ou d’un constituant)(*) .
■ Pour un système invariant ( v = 0 ), tous les paramètres sont naturellement fixés et dépendants ; toute
modification de l’un d’eux provoque une rupture d’équilibre (doc. 1).
■ Dans un système monovariant ( v = 1 ), l’équilibre est déterminé en fixant un paramètre dont dépendent
tous les autres. Modifier l’un d’eux en bloquant tous les autres provoque nécessairement une rupture
d’équilibre (doc. 2).