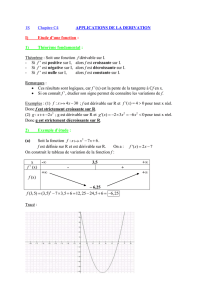
228 - Continuité et dérivabilité des fonctions

ARa
A I Rf:A→R
f a W f(a)V a
f(V∩A)⊂W
f a f A ∩[a, +∞[
A∩]− ∞, a]a
f A f
a
DRD=Zf:D→R
R R\Z
Q R\Q
fR\Q Q f(x)=0 x∈R\Q
1
qx=p q
f A\{a}l a
f˜ f f A\{a}l a
f a f a
a
f f a
f f(a−0) = sup{f(x), x < a}f(a+ 0) = inf{f(x), x > a}
f:x7→ sin 1
x0
f:A→R

A f
f(x) =
P{n/rn6x}1
2nrnf
[0,1] f(x) = 1
qx=p q∈Q
f(x) = 0 Q∩[0,1]
f a
(xn)A a f(xn)→f(a)
(xn)A a (f(xn))
f f
R R
f: [a, b]→Rf(a)f(b)<0c∈]a, b[
f(c) = 0
f I f f
f I f f
f I J f−1
f a limx→a,x∈A\{a}f(x)−f(a)
x−a
f0(a)a
a f0
d(a)f0
g(a)
a
a
x7→ |x|0

IRf:I→R
f I x, y ∈I x < y f0
g(x)6f0
d(x)6
f(y)−f(x)
y−x6f0
g(y)6f0
d(y)
f I f 0
g(x) = f0
d(x)f x
f:I→Rf−1
f(x) = x3Rf0
f−1
f:I→Ra∈I f I\{a}f0
l a f a f0(a) = l
f(x) = x x 6x+ 1 x > 0
0f0
f0l a f a f0
d(a) = l
f:I→RI
f a f0(a)
fRf(x) = x2sin 1
xx6= 0 f(0) = 0 f
Rf00
C1
f:]a, b]→R]a, b[f0
d
limx→af(x)Ri.e. f a
f0
d(x)→l x →a f a
f:I→Rn I f0, . . . , fn
IRf0=f i ∈[[0, n −1]] fif0
i=fi+1
fCnn f(n)
C∞Cnn∈N∗
f g n a fg
(fg)(n)(a) = Pn
k=0 n
kf(k)(a)g(n−k)(a)
a, b, c, d a < b < c < d
f∈ C∞(R) 0 1 1 [b, c] [a, d]
(an)u∈ C∞(R)
u(n)(0) = ann∈N
0
u∈ C∞(R)u(n)(0) = (n!)2
n∈NuP∞
n=0 n!xn0

n x1, . . . , xn
f= 1lQQn
i=1(x−xi)2
f(x)−f(xi) = (x−xi)2
E[0,1]
A E [0,1]
E
g2 [−1,1] |x|
f:x7→ Pn=0 3
4ng(4nx)R R
[0,1]
f: [a, b]→R[a, b] ]a, b[f(a) =
f(b)c∈]a, b[f0(c) = 0
PRP0
f: [a, +∞[→Ra f(x)→0
x→+∞f]a, +∞[f0]a, +∞[
f: [a, b]→R[a, b] ]a, b[
c∈]a, b[f(b)−f(a) = f0(c)(b−a)
f:I→Rf0f
f0f
I f R∗f(x) = −1
x
f(1) = −1< f(−1) = 1 R∗
f:I→Rf0(I)