EQUATION DE LA TANGENTE EN UN POINT Soit f une

EQUATION DE LA TANGENTE EN UN POINT
Soit f une fonction dérivable sur un intervalle I, et a un réel appartenant à I.
On se souvient que
f ' a
est le coefficient directeur de la tangente à la courbe représentative de
f au point d’abscisse a. Par conséquent, cette tangente a une équation de la forme
y=m xp
.
où
m=f ' a
et p est l’ordonnée à l’origine.
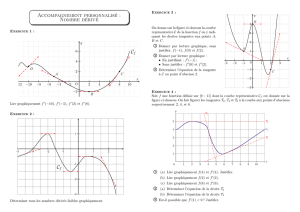
Exemple 1 : Soit f la fonction définie sur [ -3 ; 5 ] dont la courbe représentative est donnée ci-
dessous. On a tracé les tangentes à la courbe aux points d’abscisses -2 et 2.
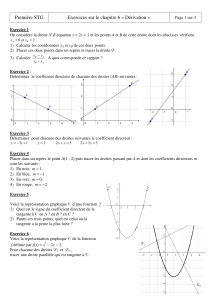
Exemple 2 : Soit f la fonction définie sur [ -1,5 ; 2,2 ] par
fx= 1
2x23 2x2
dont la courbe
représentative ( C ) est donnée ci-dessous.
•Calculer
f ' x
. En déduire
f ' 1
.
•En déduire le tracé précis de la tangente à ( C ) au point d’abscisse 1. Donner son équation
sous la forme
y=m xp
.
-1 1 2
1
2
3
4
5
6
7
x
y
x
y
-2 -1 0 1 2 3 4
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
Déterminer graphiquement
f ' −2
et
f ' 2
.
Donner l'équation des tangentes à la courbe
aux points d'abscisse -2, puis 2.

Il n’est pas toujours possible de déterminer graphiquement l’équation d’une tangente (manque de
précision, ou l’ordonnée à l’origine n’est pas lisible, etc…). Mais nous disposons du :
THEOREME : Une équation de la tangente à la courbe représentative de f au point d’abscisse a
peut s’écrire sous la forme :
y=f ' a x−a fa
.
Exemple : Soit f la fonction définie sur
[−20 ;20]
par
fx=x2−3x4
. On cherche à
déterminer l’équation de la tangente à la courbe représentative de f au point d’abscisse 1.
•
f1=12−3×14=2
.
•
f ' x=2x−3
, donc
f ' 1=2×1−3=−1
•D’après le théorème précédent, l’équation de la tangente à la courbe représentative de f au
point d’abscisse 1 peut s’écrire sous la forme :
y=f ' 1 x−1 f1
, soit
y=− x−12
, c’est-à-dire
y=−x12
,
Finalement :
y=−x3
.
SENS DE VARIATION D’ UNE FONCTION
Le but de ce cours se situe dans ce chapitre : donner le lien intime entre la fonction f et sa dérivée
f '
. Le mot clé est VARIATIONS. Ceci sert notamment à résoudre des problèmes
d’optimisation. Imaginons par exemple un producteur cherchant à dégager un bénéfice maximal de
son exploitation. Il est évident de dire que ce n’est pas parce qu’il produira plus qu’il gagnera plus
d’argent. En effet, produire davantage signifie aussi avoir plus de frais ! Il faut donc chercher
l’équilibre optimal entre : gains rapportés par la production et frais dus à la production. Les outils
présentés dans ce chapitre vont nous permettre de répondre à cette question dans certains cas.
Pour le moment, découvrons les liens entre une fonction f et sa dérivée
f '
.
Exemple : Soit f une fonction définie sur [ -6 ; 5 ] dont la courbe représentative ( C ) est donnée ci-
dessous. On a représenté en divers points les tangentes à la courbe.
-6 -5 -4 -3 -2 -1 1 2 3 4 5
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
y
A
B
CD
•Dresser le tableau de variations de f . Préciser les intervalles sur lesquels f est croissante et
ceux sur lesquels f est décroissante.

•Donner le signe des nombres dérivés
f ' −6
,
f ' −4
,
f ' −1
et
f ' 3
.
•Faîtes une hypothèse entre le signe de
f ' x
sur un intervalle et le sens de variation de f
sur ce même intervalle.
THEOREME : Soit f une fonction dérivable sur un intervalle I.• Si quelque soit x appartenant à I,
f ' x=0
, alors f est constante sur I ;
•Si quelque soit x appartenant à I, sauf éventuellement en quelques points où la fonction f'
s'annule on a
f ' x0
, alors f est strictement croissante sur I ;
•Si quelque soit x appartenant à I, sauf éventuellement en quelques points où la fonction f'
s'annule on a
f ' x0
, alors f est strictement décroissante sur I.
Application : Soit f la fonction définie sur
ℝ
par
fx=3x2−2x4
•Calculer
f ' x
•Étudier le signe de
f ' x
•En déduire les variations de f. (résumer sous la forme d’un tableau de variations)