DS N°8 Lundi 7 Janvier 2013.pdf

1S3 Lundi 7 Janvier 2013
DS N°5 : DERIVATION et APPLICATIONS
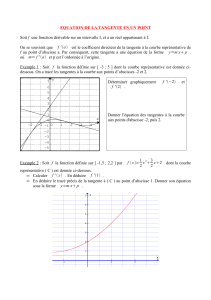
1 La courbe en rouge ci-contre représente une fonction dérivable sur IR et admet une tangente aux points A, E et B.
Déterminez graphiquement :
a. f (–1)
b. f (0)
c. f (1)
d. f ’ (–1)
e. f ’ (0)
f. f ’ (1)
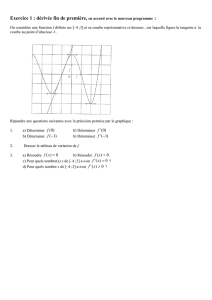
2 .
Soit
f:x1
2x32x1
la fonction définie sur IR et (C) sa courbe représentative représentée
ci-contre.
On considère deux points de (C), A et B, d’abscisse respective –2 et 0.
1. Vérifiez par le calcul que
f2
 f0   1
.
2. Calculez
f'(x).
3. En déduire une équation des droites TA et TB, tangentes à C respectivement en A et en B.
3 .On considère la fonction inverse :
f:x1
x
définie sur IR* et H sa courbe représentative
sur
]0; [
.
Soit M un point d’abscisse a appartenant à la courbe H.
La tangente T à C au point M coupe l’axe des ordonnées en A et l’axe des abscisses en B.
1. Écrivez, en fonction de a, une équation de T.
2. Calculez, en fonction de a, les coordonnées des points A et B.
3. En déduire que le point M est le milieu du segment [AB].
4 Soit
f:x x26x7
une fonction définie sur IR et C sa courbe représentative ci-contre.
M5
2;4
est un point du plan.
1. a. Calculez
f'x
.
b. Montrez que la tangente T à C au point d’abscisse a admet comme équation :
y2a6
 x7a2
.
2. a. Démontrez que la droite T passe par le point M
si et seulement si a vérifie l’équation :
a25a40
.
b. Résolvez cette équation puis en déduire l’équation des deux tangentes à C passant par
le point M.
5 .
Soit f une fonction trinôme définie sur IR par
f(x)ax2bxc
et C sa courbe représentative.
C coupe l’axe des ordonnées en y = –3 et admet une tangente horizontale au point A(1 ; 4).
1. Traduisez les informations par un système d’équations.
2. En déduire les valeurs des réels a, b et c.