Exercice 1 : dérivée fin de première, en accord avec le nouveau

Exercice 1 : dérivée fin de première, en accord avec le nouveau programme :
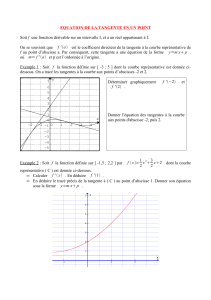
On considère une fonction f définie sur [–4 ;3] et sa courbe représentative ci-dessous , sur laquelle figure la tangente à la
courbe au point d’abscisse–1.
Répondre aux questions suivantes avec la précision permise par le graphique :
1. a) Déterminer )0(fb) Déterminer )0('f
b) Déterminer )1(
−
fb) Déterminer )1('
−
f
2. Dresser le tableau de variation de f.
3. a) Résoudre 0)(
=
xf b) Résoudre 0)(
>
xf .
c) Pour quels nombre(s) x de [–4 ;3] a-t-on 0)('
=
xf ?
d) Pour quels nombre x de [–4 ;3] a-t-on 0)('
>
xf ?

Exercice 2 :analyse fin de première , en accord avec le nouveau programme
Partie A
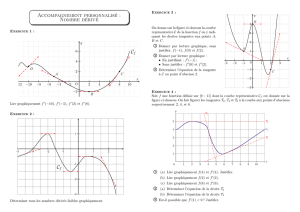
On considère la courbe représentative C d’une fonction f dans le repère ci-dessous.
Les points E(–3 ;0) , F(0 ;–3) et G(1,0) sont sur C. La droite d’équation 72
−
−
=
xy est tangente à C au point A d’abscisse–2. La
tangente à C au point S(–1 ;–4) est parallèle à l’axe des abscisses.
1) QCM : entourer la ou les bonnes réponses :
l’image de –3 par f est 0 –3 1
dans [–5 ;5], l’équation 5)(
=
xf a0 solution 1 solution 2 solutions
dans [–5 ;5], l’équation 5)(
−
=
xf a0 solution 1 solution 2 solutions
la droite (EF) a pour coefficient directeur –3 1 –1
l’inéquation 0)(
<
xf a pour solution ]-3 ;1[ ]-2 ;0[ [–3 ;1]
la tangente à C au point S a pour équation: 4
−
=
y xy 4
−
=
4
−
=
x
)2('
−
f vaut –2 –7 –3
2) La tangente à C au point d’abscisse 0 passe par D(–2 ;–7). En déduire )0('f
Partie B :
la fonction f représentée ci dessus est définie sur R par : 32²)(
−
+
=
xxxf . On considère la fonction g définie sur R par :
1²2)(
+
+
−
=
xxxg .
1. Construire la courbe C’ représentative de g dans le repère précédent.
2. Déterminer ( par le calcul) )2('g. En déduire l’équation de la tangente à C’ au point B d’abscisse 2.
3. Résoudre graphiquement, l’équation )()( xgxf
=
4a. développer )1)(43(
−
+
xx .
b. Résoudre ,par le calcul, l’équation )()( xgxf
=
.
o
E
F
S
G
A

Exercice 3 : analyse fin de terminale , en accord avec le nouveau programme: ( option 3heures)
QCM : Pour chaque question, donner la ou les bonnes réponses.
1. Soit f définie sur R par 16²3)(
+
−
=
xxxf . Une équation de la tangente à la courbe de f au point d’abscisse 2 est :
12
+
=
xy 116
−
=
xy 16
+
=
xy
2. Soit une fonction f définie et dérivable sur [–12 ;20]. On donne dans le tableau ci-dessous le signe de f’
x–12 –5 7 20
signe de f’ – 0 + 0 –
On peut dire que :
f est croissante sur [–12 ;20] f est décroissante sur [–12 ; –5] f est décroissante sur [–12 ; –5] et
[7 ; 20]
3. Voici le tableau de variation d’une fonction f définie sur [–12 ;20] :
x–12 –5 7 20
variations de f
7 0
–4 –6
a) On peut dire que :
f est positive [–12 ;–5] f est positive [7 ;20] f est négative sur [–5 ;20]
b) L’équation 5)(
−
=
xf possède
une unique solution aucune solution on ne peut pas répondre
c) Comparaison de f(0) et f(8) :
)8()0( ff
<
)8()0( ff
>
on ne peut pas répondre
4. Soit f définie pour 4
≠
x par
4
3
)(
−
+
=
x
x
xf
. Alors ...)('
=
xf
( ) ²412 −
−
xx
4
7
−
−
x
)²4( 7 −
−
x
5. Soit f définie sur I=
+∞−
;
2
1 par )12ln()(
+
=
xxf . Alors :
f est croissante sur I f est décroissante sur I f n’est ni croissante ni décroissante sur I
6. Si
y
x
>
alors :
yx 25,025,0 >yx 25,025,0 <on ne peut pas comparer x
25,0
et y
25,0 .
7. Un capital est placé à un taux annuel de 3,5% pendant 10 ans à intérêts composées.
Le capital est multiplié en 10 ans par environ :
1,41 1,35 1,035