B mecanique
1
Plan du cours
•Introduction
•Notions de mécanique : force, énergie, travail,
puissance…
•Température et chaleur
•Systèmes, transformations et échanges thermodynamiques
•Premier principe de la thermodynamique
•Second principe de la thermodynamique
•Brève introduction aux probabilités et à la statistique
•Notions élémentaires de mécanique statistique
• Théorie de l’information
Placez le curseur sur l’illustration dont vous désirez connaître l’origine.
2
Mécanique
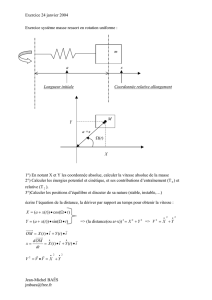
Afin de pouvoir étudier les liens entre chaleur et travail,
nous commencerons par introduire les concepts nécessaires
à l’étude du travail mécanique : force, travail, énergie…
3
Force
L’action exercée par une force en un point d’un corps peut
être assimilée à la traction d’un fil attaché en ce point. Elle
possède les caractéristiques suivantes :
•une direction, celle du fil,
•un sens, celui de la traction exercée sur le fil,
• un point d’application,
•une grandeur, la tension exercée sur le fil.
Il s’agit donc d’un vecteur.
On appelle résultante la somme des forces appliquées à un
corps.
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
1
/
40
100%
