Géométrie dans l`espace - ambition

1
TS / mathématiques Mme MAINGUY
Terminale S
Géométrie dans l'espace
Ch.6
 La perspective cavalière
C'est un ensemble de règles permettant de représenter un volume dans un plan; ce n'est pas ce que nous
voyons dans la réalité. En effet, en perspective cavalière :
● deux droites parallèles dans la réalité sont représentées par des droites parallèles ;
● les milieux des segments et les rapports de longueur sont conservés ;
● les longueurs et les angles ne sont en général pas conservés ;
● les arêtes cachées sont représentées en pointillés.
I. Règles de base de la géométrie dans l'espace
 Règle 1
Il existe une et une seule droite de l'espace passant par deux points distincts.
 Règle 2
Il existe un et un seul plan de l'espace passant par trois points non alignés.
 Théorème
Si deux plans distincts ont un point commun, alors leur intersection est une droite.
exemple : le livre ouvert
 Définition
Quatre points (ou plus) appartenant à un même plan sont dits "coplanaires".
Deux droites ou plus appartenant à un même plan sont dites "coplanaires".
 Règle 3
Quand tous les éléments (points, droites, ...) d'un problème de l'espace sont coplanaires, toutes les règles de
géométrie plane s'appliquent (Thalès, Pythagore, etc...)
On comprendra mieux les règle 2 et définition en donnant les analogies dans le plan :
Par deux points, il passe une droite et une seule.
Trois points appartenant à une même droite sont dits "alignés".
Exercice 1
P
est un plan.
A , B , C
sont trois points non alignés qui n'appartiennent pas à
P
.
On suppose que
AB
coupe
P
en
C
, que
AC
coupe
P
en
B
et que
BC
coupe
P
en
A
.
Montrer que les points
A , B , C
sont alignés.
Solution
●
A , B , C
sont trois points non alignés n'appartenant pas à
P
donc (règle 2), il existe un unique plan
P
contenant
ces trois points.
● Comme
A et B
sont deux points de
P
, alors la droite
AB
est contenue dans
P
. De la même façon, on peut
affirmer que
AC
et
BC
sont incluses dans
P
.
●
A
est un point commun à
P
et
P
donc l'intersection de ces deux plans est une droite passant par
A
(théorème).
B
et
C
étant communs à
P
et
P
, l'intersection de
P
et
P
est une droite passant par ces deux points.
On en déduit que l'intersection de
P
et
P
est une droite passant par les trois points
A , B et C
qui sont donc alignés.

2
TS / mathématiques Mme MAINGUY
II. Positions relatives de droites et de plans de l'espace
 Positions relatives de deux droites
Deux droites de l'espace sont soit coplanaires, soit non coplanaires.
Si elles sont coplanaires (dans un même plan), Si elles sont non coplanaires,
on distingue alors trois cas : aucun plan ne les contient
elles peuvent être : toutes les deux.
● sécantes ● strictement parallèles ● confondues
elles ont un seul point elles n'ont aucun point leur intersection est vide
commun commun
Remarque
Attention: dans l'espace, deux droites n'ayant aucun point commun ne sont donc pas toujours parallèles.
Schématisation
non coplanaires coplanaires
sécantes parallèles
confondues srictement parallèles
 Positions relatives d'une droite et d'un plan
Une droite et un plan de l'espace sont soit sécants, soit parallèles.
● sécants ● parallèles
d
et P ont un point d'intersection : B
d
et P sont strictement parallèles,
d
est contenue dans P .
leur intersection est vide.

3
TS / mathématiques Mme MAINGUY
Schématisation
la droite et le plan la droite est parallèle au plan
sont sécants
la droite est strictement la droite est contenue
parallèle au plan dans le plan
 Positions relatives de deux plans
Deux plans de l'espace sont soit sécants, soit parallèles.
● sécants ● parallèles
P et P ' ont une droite d'intersection :
d
P et P ' sont strictement parallèles, P et P ' sont confondus.
leur intersection est vide.
Ainsi, deux plans sont parallèles lorsqu'ils ne sont pas sécants.
Schématisation
sécants parallèles
strictement parallèles confondus
Exercice 2
Dans le cube ABCDEFGH, on note I le milieu de [AB], J le milieu de [DH], K le
milieu de [HG] et L le milieu de [EF].
Quelle est la nature de l'intersection des plans (IJK) et (BCL) ?
Solution
● Dans le plan (FGH) : K milieu de [HG] et L milieu de [FE]. Or HG = EF
On en déduit que GK = FL.
De plus comme (GH) // (FE) alors on a aussi (GK) // (FL)
On peut donc conclure que GKFL est un parallélogramme;
Ses côtés sont parallèles deux à deux d'où (KL) // (GF)
De même, on justifie que (DA) // (IJ)
Ainsi : (KL) // (GF) // (BC) // (DA) // (IJ)
● Le plan (BCL) contient la droite passant par L et parallèle à (BC) : c'est (KL).
De même, le plan (IJK) contient la droite passant par K et parallèle à (IJ) : c'est (KL)
● Les deux plans (BCL) et (IJK) n'étant pas confondus, l'intersection de ces deux plans
est la droite (KL)

4
TS / mathématiques Mme MAINGUY
III. Parallélisme dans l'espace
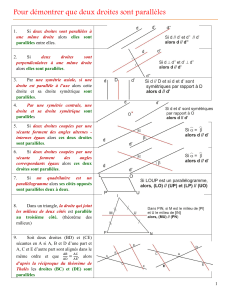
 Parallélisme de droites : propriétés admises
P1 Si deux droites sont parallèles, alors toute parallèle à l'une est parallèle à l'autre.
P2 Si deux droites sont parallèles, tout plan qui coupe l'une coupe l'autre.
 Parallélisme de plans : propriétés admises
P3 Si deux plans sont parallèles, alors tout plan parallèle à l'un est parallèle à l'autre.
// //
//
PPP
PP
P
P4 Si deux droites sécantes
1
d
et
2
d
d'un plan P sont parallèles à un
plan P ' , alors P et P ' sont parallèles.
12
12
12
//
// //
et
et secantes
et
dd
dd
dd
PP
PP
PP
P5 Si deux plans P et P ' sont parallèles, alors tout plan qui coupe P , coupe
aussi P ' et les droites d'intersection
d
et
d
sont parallèles.
// // d
dd
d
P
PP
P
 Parallélisme d'une droite et d'un plan : propriétés admises
P6 Si une droite est parallèle à une droite
d
contenue dans
un plan P alors et P sont parallèles.
// // d
d
P
P
P7 Si une droite
d
est parallèle à deux plans P et P ' sécants suivant une
droite , alors
d
et sont parallèles.
// // // et d dd PP
P P =
Théorème du toit
1
d
et
2
d
sont deux droites parallèles,
1
d
contenue dans P1 et
2
d
contenue dans P2.
Si deux plans P1 et P2 sont sécants, alors leur droite commune
est parallèle à
1
d
et
2
d
.
12
1 2 1 2
// // //
et
d et d
dd
dd
=
P1 P2
P1 P2

5
TS / mathématiques Mme MAINGUY
IV. Orthogonalité dans l'espace
1 / droites orthogonales
 Définition
Dans l'espace, dire que deux droites
1
d
et
2
d
sont orthogonales
signifie qu'on peut trouver un point
I
tel que les parallèles à ces droites
passant par
I
sont perpendiculaires.
On écrit
12
dd
 Théorème (admis)
Si deux droites sont parallèles alors toute orthogonale à l'une
est orthogonale à l'autre.
12 2
1
//dd d
d
On écrit
12
dd
2 / droites perpendiculaires à un plan
 Définition
I
est l'intersection d'une droite
d
et d'un plan
P
.
Dire que
d
et
P
sont perpendiculaires signifie que
d
est
perpendiculaire à deux droites
1
d
et
2
d
de
P
passant par
I
.
Remarque
On admet alors que
d
est perpendiculaire à toute droite de
P
passant par
I
.
 Théorème
Si une droite
d
est perpendiculaire à un plan
P
, alors
d
est
orthogonale à toute droite contenue dans
P
.
Démonstration
Soit une droite contenue dans le plan
P
.On veut montrer que
d
est perpendiculaire à .
d
étant perpendiculaire à
P
alors
d
est en particulier perpendiculaire à
1
, droite de
P
sécante à
d
en
I
et parallèle à .
Ainsi :
1
1
// d
d
d
est donc orthogonale à .